Los residentes del sureste de los Estados Unidos están muy familiarizados con los gráficos, conocidos como modelos de espagueti, como el de la Figura ( PageIndex {1} ). Combinan una colección de datos meteorológicos para predecir el camino más probable de un huracán. Cada línea de color representa un camino posible. El grupo de líneas onduladas puede comenzar a parecerse a hebras de espagueti, de ahí su nombre. En esta sección, investigaremos métodos para hacer este tipo de predicciones.
Construyendo modelos de probabilidad
Supongamos que tiramos un cubo numérico de seis lados. Lanzar un cubo de números es un ejemplo de un experimento , o una actividad con un resultado observable. Los números en el cubo son posibles resultados, o resultados , de este experimento. El conjunto de todos los resultados posibles de un experimento se denomina espacio de muestra del experimento. El espacio muestral para este experimento es ( {1,2,3,4,5,6 } ). Un evento es cualquier subconjunto de un espacio muestral.
La probabilidad de un evento se conoce como probabilidad. La probabilidad de un evento pp es un número que siempre satisface (0≤p≤1 ), donde (0 ) indica un evento imposible y (1 ) indica un evento determinado. Un modelo de probabilidad es una descripción matemática de un experimento que enumera todos los resultados posibles y sus probabilidades asociadas. Por ejemplo, si hay una probabilidad de (1 % ) de ganar un sorteo y una probabilidad de (99 % ) de perder el sorteo, un modelo de probabilidad se parecería mucho a la Tabla ( PageIndex {1} )
| Resultado | Probabilidad |
|---|---|
| Ganar el sorteo | 1% |
| Perder el sorteo | 99% |
La suma de las probabilidades enumeradas en un modelo de probabilidad debe ser igual a (1 ) o (100 % ).
Cómo: dado un evento de probabilidad donde cada evento es igualmente probable, construir un modelo de probabilidad.
- Identifica cada resultado.
- Determine el número total de posibles resultados.
- Compare cada resultado con el número total de resultados posibles.
Ejemplo ( PageIndex {1} ): Construcción de un modelo de probabilidad
Construya un modelo de probabilidad para lanzar un dado único y justo, siendo el evento el número que se muestra en el dado.
Solución
Comience haciendo una lista de todos los resultados posibles para el experimento. Los posibles resultados son los números que se pueden obtener: (1 ), (2 ), (3 ), (4 ), (5 ) y (6 ). Hay seis resultados posibles que conforman el espacio muestral.
Asigne probabilidades a cada resultado en el espacio muestral determinando una relación del resultado al número de resultados posibles. Hay uno de cada uno de los seis números en el cubo, y no hay razón para pensar que es más probable que aparezca una cara en particular que cualquier otra, por lo que la probabilidad de sacar cualquier número es (16 ).
| Resultado | Rollo de 1 | Rollo de 2 | Rollo de 3 | Rollo de 4 | Rollo de 5 | Rollo de 6 |
|---|---|---|---|---|---|---|
| Probabilidad | ( dfrac {1} {6} ) | ( dfrac {1} {6} ) | ( dfrac {1} {6} ) | ( dfrac {1} {6} ) | ( dfrac {1} {6} ) | ( dfrac {1} {6} ) |
P y R: ¿Las probabilidades siempre tienen que expresarse como fracciones?
No. Las probabilidades se pueden expresar como fracciones, decimales o porcentajes. La probabilidad siempre debe ser un número entre (0 ) y (1 ), incluido (0 ) y (1 ).
Calculando las probabilidades de resultados igualmente probables
Sea (S ) un espacio de muestra para un experimento. Al investigar la probabilidad, un evento es cualquier subconjunto de (S ). Cuando los resultados de un experimento son todos igualmente probables, podemos encontrar la probabilidad de un evento dividiendo el número de resultados en el evento por el número total de resultados en (S ). Supongamos que se lanza un cubo numérico y estamos interesados en encontrar la probabilidad de que el evento “arroje un número menor o igual a 4”. Hay 4 resultados posibles en el evento y 6 resultados posibles en (S ), por lo que la probabilidad del evento es ( dfrac {4} {6} = dfrac {2} {3} ).
COMPUTACIÓN DE LA PROBABILIDAD DE UN EVENTO CON RESULTADOS IGUALMENTE PROBABLES
La probabilidad de un evento (E ) en un experimento con espacio muestral (S ) con resultados igualmente probables viene dada por
[P (E) = dfrac { text {número de elementos en} E} { text {número de elementos en} S} = dfrac {n (E)} {n (S)} ]
(E ) es un subconjunto de (S ), por lo que siempre es cierto que (0≤P (E) ≤1 ).
Ejemplo ( PageIndex {2} ): Calcular la probabilidad de un evento con resultados igualmente probables
Se rueda un cubo numérico. Encuentre la probabilidad de sacar un número impar.
Solución
El evento “obtener un número impar” contiene tres resultados. Hay (6 ) resultados igualmente probables en el espacio muestral. Divide para encontrar la probabilidad del evento.
(P (E) = dfrac {3} {6} = dfrac {1} {2} )
Ejercicio ( PageIndex {1} )
Se rueda un cubo numérico. Encuentre la probabilidad de obtener un número mayor que (2 ).
- Respuesta
-
( dfrac {2} {3} )
Calculando la probabilidad de la unión de dos eventos
A menudo estamos interesados en encontrar la probabilidad de que ocurra uno de los múltiples eventos. Supongamos que estamos jugando un juego de cartas y ganaremos si la siguiente carta robada es un corazón o un rey. Nos interesaría encontrar la probabilidad de que la próxima carta sea un corazón o un rey. La unión de dos eventos (E ) y (F ), escritos (E cup F ), es el evento que ocurre si uno o ambos eventos ocurren.
[P (E copa F) = P (E) + P (F) −P (E cap F) ]
Suponga que la ruleta de la Figura ( PageIndex {2} ) está girada. Queremos encontrar la probabilidad de girar naranja o girar a (b ).
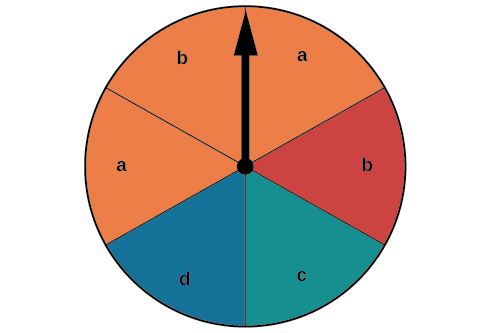
Hay un total de (6 ) secciones, y (3 ) de ellas son de color naranja. Entonces la probabilidad de girar naranja es ( dfrac {3} {6} = dfrac {1} {2} ). Hay un total de (6 ) secciones, y (2 ) de ellas tienen un (b ). Entonces, la probabilidad de girar a (b ) es ( dfrac {2} {6} = dfrac {1} {3} ). Si agregamos estas dos probabilidades, estaríamos contando el sector que es naranja y a (b ) dos veces. Para encontrar la probabilidad de girar una naranja o una (b ), necesitamos restar la probabilidad de que el sector sea naranja y tenga una (b ).
( dfrac {1} {2} + dfrac {1} {3} – dfrac {1} {6} = dfrac {2} {3} )
La probabilidad de girar naranja o a (b ) es ( dfrac {2} {3} ).
PROBABILIDAD DE LA UNIÓN DE DOS EVENTOS
La probabilidad de la unión de dos eventos (E ) y (F ) (escrita (E cup F )) es igual a la suma de la probabilidad de (E ) y la probabilidad de (F ) menos la probabilidad de que (E ) y (F ) ocurran juntas (que se llama la intersección de (E ) y (F ) y se escribe como (E cap F )).
[P (E copa F) = P (E) + P (F) −P (E cap F) ]
Ejemplo ( PageIndex {3} ): Calcular la probabilidad de la unión de dos eventos
Se extrae una carta de un mazo estándar. Encuentre la probabilidad de dibujar un corazón o un (7 ).
Solución
Una baraja estándar contiene el mismo número de corazones, diamantes, tréboles y espadas. Entonces, la probabilidad de dibujar un corazón es ( dfrac {1} {4} ). Hay cuatro (7s ) en un mazo estándar, y hay un total de (52 ) cartas. Entonces, la probabilidad de sacar un (7 ) es ( dfrac {1} {13} ).
La única carta en el mazo que es tanto un corazón como un (7 ) es el (7 ) de corazones, por lo que la probabilidad de sacar tanto un corazón como un (7 ) es ( dfrac {1} {52} ). Sustituir (P (H) = dfrac {1} {4} ), (P (7) = dfrac {1} {13} ) y (P (H cap 7) = dfrac {1} {52} ) en la fórmula.
[ begin {align *} P (E cup F) & = P (E) + P (F) −P (E cap F) \ [4pt] & = dfrac {1} { 4} + dfrac {1} {13} – dfrac {1} {52} \ [4pt] & = dfrac {4} {13} end {align *} ]
La probabilidad de dibujar un corazón o un (7 ) es ( dfrac {4} {13} ).
Ejercicio ( PageIndex {2} )
Se extrae una carta de un mazo estándar. Encuentre la probabilidad de sacar una tarjeta roja o un as.
- Respuesta
-
( dfrac {7} {13} )
Cálculo de la probabilidad de eventos mutuamente excluyentes
Suponga que la ruleta de la Figura ( PageIndex {2} ) se gira nuevamente, pero esta vez estamos interesados en la probabilidad de girar una naranja o una (d ). No hay sectores que sean anaranjados y contengan un (d ), por lo que estos dos eventos no tienen resultados en común. Se dice que los eventos son eventos mutuamente excluyentes cuando no tienen resultados en común. Como no hay superposición, no hay nada que restar, por lo que la fórmula general es
[P (E cap F) = P (E) + P (F) ]
Observe que con eventos mutuamente excluyentes, la intersección de (E ) y (F ) es el conjunto vacío. La probabilidad de girar una naranja es ( dfrac {3} {6} = dfrac {1} {2} ) y la probabilidad de girar una (d ) es ( dfrac {1} {6} ). Podemos encontrar la probabilidad de girar una naranja o una (d ) simplemente sumando las dos probabilidades.
[ begin {align *} P (E cap F) & = P (E) + P (F) \ [4pt] & = dfrac {1} {2} + dfrac {1} {6} \ & = dfrac {2} {3} end {align *} ]
La probabilidad de girar una naranja o una (d ) es ( dfrac {2} {3} ).
PROBABILIDAD DE LA UNIÓN DE EVENTOS MUTUAMENTE EXCLUSIVOS
La probabilidad de la unión de dos eventos mutuamente excluyentes [(E ) y (F ) viene dada por
[P (E cap F) = P (E) + P (F) ]
Cómo: dado un conjunto de eventos, calcular la probabilidad de la unión de eventos mutuamente excluyentes.
- Determine el número total de resultados para el primer evento.
- Encuentre la probabilidad del primer evento.
- Determine el número total de resultados para el segundo evento.
- Encuentre la probabilidad del segundo evento.
- Suma las probabilidades.
Ejemplo ( PageIndex {4} ): Calcular la probabilidad de la unión de eventos mutuamente excluyentes
Se extrae una carta de un mazo estándar. Encuentre la probabilidad de dibujar un corazón o una espada.
Solución
Los eventos “dibujar un corazón” y “dibujar una espada” son mutuamente excluyentes porque no pueden ocurrir al mismo tiempo. La probabilidad de dibujar un corazón es ( dfrac {1} {4} ), y la probabilidad de dibujar una espada también es ( dfrac {1} {4} ), por lo que la probabilidad de dibujar un corazón o una pala es
( dfrac {1} {4} + dfrac {1} {4} = dfrac {1} {2} )
Ejercicio ( PageIndex {3} )
Se extrae una carta de un mazo estándar. Encuentra la probabilidad de sacar un as o un rey.
- Respuesta
-
( dfrac {2} {13} )
Usando la regla del complemento para calcular las probabilidades
Hemos discutido cómo calcular la probabilidad de que ocurra un evento. A veces, estamos interesados en encontrar la probabilidad de que un evento no suceda. El complemento de un evento (E ), denotado (E ′ ), es el conjunto de resultados en el espacio muestral que no están en (E ). Por ejemplo, supongamos que estamos interesados en la probabilidad de que un caballo pierda una carrera. Si el evento (W ) es el caballo que gana la carrera, entonces el complemento del evento (W ) es el caballo que pierde la carrera.
Para encontrar la probabilidad de que el caballo pierda la carrera, necesitamos usar el hecho de que la suma de todas las probabilidades en un modelo de probabilidad debe ser (1 ).
[P (E ‘) = 1 − P (E) ]
La probabilidad de que el caballo gane sumada a la probabilidad de que el caballo pierda debe ser igual a (1 ). Por lo tanto, si la probabilidad de que el caballo gane la carrera es ( dfrac {1} {9} ), la probabilidad de que el caballo pierda la carrera es simplemente
(1− dfrac {1} {9} = dfrac {8} {9} )
LA REGLA DE COMPLEMENTO
La probabilidad de que ocurra el complemento de un evento viene dada por
[P (E ‘) = 1 − P (E) ]
Ejemplo ( PageIndex {5} ): Uso de la regla del complemento para calcular las probabilidades
Se ruedan dos cubos numéricos de seis lados.
- Encuentre la probabilidad de que la suma de los números obtenidos sea menor o igual que (3 ).
- Encuentre la probabilidad de que la suma de los números obtenidos sea mayor que (3 ).
Solución
El primer paso es identificar el espacio muestral, que consiste en todos los resultados posibles. Hay dos cubos numéricos, y cada cubo numérico tiene seis resultados posibles. Usando el Principio de Multiplicación, encontramos que hay (6 × 6 ), o (36 ) resultados totales posibles. Entonces, por ejemplo, (1-1 ) representa un (1 ) enrollado en cada cubo numérico.
| (1-1 ) | (1-2 ) | (1-3 ) | (1-4 ) | (1-5 ) | (1-6 ) |
| (2-1 ) | (2-2 ) | (2-3 ) | (2-4 ) | (2-5 ) | (2-6 ) |
| (3-1 ) | (3-2 ) | (3-3 ) | (3-4 ) | (3-5 ) | (3-6 ) |
| (4-1 ) | (4-2 ) | (4-3 ) | (4-4 ) | (4-5 ) | (4-6 ) |
| (5-1 ) | (5-2 ) | (5-3 ) | (5-4 ) | (5-5 ) | (5-6 ) |
| (6-1 ) | (6-2 ) | (6-3 ) | (6-4 ) | (6-5 ) | (6-6 ) |
- Necesitamos contar la cantidad de formas de obtener una suma de (3 ) o menos. Estos incluirían los siguientes resultados: (1-1 ), (1-2 ) y (2-1 ). Por lo tanto, solo hay tres formas de obtener una suma de (3 ) o menos. La probabilidad es
( dfrac {3} {36} = dfrac {1} {12} )
- En lugar de enumerar todas las posibilidades, podemos usar la regla del complemento. Como ya hemos encontrado la probabilidad del complemento de este evento, simplemente podemos restar esa probabilidad de (1 ) para encontrar la probabilidad de que la suma de los números obtenidos sea mayor que (3 ).
[ begin {align *} P (E ‘) & = 1-P (E) \ & = 1- dfrac {1} {12} \ & = dfrac {11} {12} end {align *} ]
Ejercicio ( PageIndex {4} ):
Se ruedan dos cubos numéricos. Use la regla del complemento para encontrar la probabilidad de que la suma sea menor que (10 ).
- Respuesta
-
( dfrac {5} {6} )
Probabilidad de cálculo usando la teoría de conteo
Muchos problemas de probabilidad interesantes implican contar principios, permutaciones y combinaciones. En estos problemas, utilizaremos permutaciones y combinaciones para encontrar el número de elementos en eventos y espacios de muestra. Estos problemas pueden ser complicados, pero se pueden hacer más fáciles dividiéndolos en problemas de conteo más pequeños.
Suponga, por ejemplo, que una tienda tiene (8 ) teléfonos celulares y que (3 ) de ellos están defectuosos. Es posible que deseemos encontrar la probabilidad de que una pareja que compra (2 ) teléfonos reciba (2 ) teléfonos que no son defectuosos. Para resolver este problema, necesitamos calcular todas las formas de seleccionar teléfonos (2 ) que no son defectuosos, así como todas las formas de seleccionar teléfonos (2 ). Hay (5 ) teléfonos que no son defectuosos, por lo que hay (C (5,2) ) formas de seleccionar (2 ) teléfonos que no son defectuosos. Hay (8 ) teléfonos, por lo que hay (C (8,2) ) formas de seleccionar (2 ) teléfonos. La probabilidad de seleccionar (2 ) teléfonos que no son defectuosos es:
[ begin {align *} dfrac { text {formas de seleccionar 2 teléfonos que no son defectuosos}} { text {formas de seleccionar 2 teléfonos}} & = dfrac {C (5,2) } {C (8,2)} \ [4pt] & = dfrac {10} {28} \ [4pt] & = dfrac {5} {14} end {align *} ]
Ejemplo ( PageIndex {5} ): Probabilidad de cálculo usando la teoría de conteo
Un niño selecciona aleatoriamente (5 ) juguetes de un contenedor que contiene (3 ) conejitos, (5 ) perros y (6 ) osos.
- Encuentra la probabilidad de que solo se elijan osos.
- Encuentre la probabilidad de que se elijan (2 ) osos y (3 ) perros.
- Encuentre la probabilidad de que se elijan al menos (2 ) perros.
Solución
- Necesitamos contar la cantidad de formas de elegir solo osos y la cantidad total de formas posibles de seleccionar (5 ) juguetes. Hay (6 ) osos, por lo que hay (C (6,5) ) formas de elegir (5 ) osos. Hay (14 ) juguetes, por lo que hay (C (14,5) ) formas de elegir cualquier (5 ) juguetes.
( dfrac {C (6,5)} {C (14,5)} = dfrac {6} {2,002} = dfrac {3} {1,001} )
- Necesitamos contar la cantidad de formas de elegir (2 ) osos y (3 ) perros y la cantidad total de formas posibles de seleccionar (5 ) juguetes. Hay (6 ) osos, por lo que hay (C (6,2) ) formas de elegir (2 ) osos. Hay (5 ) perros, por lo que hay (C (5,3) ) formas de elegir (3 ) perros. Como estamos eligiendo tanto osos como perros al mismo tiempo, utilizaremos el Principio de multiplicación. Hay (C (6,2) ⋅C (5,3) ) formas de elegir (2 ) osos y (3 ) perros. Podemos usar este resultado para encontrar la probabilidad.
( dfrac {C (6,2) C (5,3)} {C (14,5)} = dfrac {15⋅10} {2,002} = dfrac {75} {1,001} )
- A menudo es más fácil resolver “al menos” problemas utilizando la regla de complemento. Comenzaremos por encontrar la probabilidad de que se elijan menos de (2 ) perros. Si se eligen menos de (2 ) perros, entonces no se puede elegir ningún perro o se puede elegir (1 ) perro.
Cuando no se eligen perros, todos los juguetes (5 ) provienen de los juguetes (9 ) que no son perros. Hay (C (9,5) ) formas de elegir juguetes de los (9 ) juguetes que no son perros. Como hay (14 ) juguetes, hay (C (14,5) ) formas de elegir los juguetes (5 ) de todos los juguetes.
( dfrac {C (9,5)} {C (14,5)} = dfrac {63} {1,001} )
Si se elige (1 ) perro, entonces los juguetes (4 ) deben provenir de los (9 ) juguetes que no son perros, y (1 ) deben provenir de (5 ) perros. Dado que estamos eligiendo perros y otros juguetes al mismo tiempo, utilizaremos el Principio de multiplicación. Hay (C (5,1) ⋅C (9,4) ) formas de elegir (1 ) perro y (1 ) otro juguete.
( dfrac {C (5,1) C (9,4)} {C (14,5)} = dfrac {5⋅126} {2,002} = dfrac {315} {1,001} )
Debido a que estos eventos no ocurrirían juntos y, por lo tanto, son mutuamente excluyentes, agregamos las probabilidades para encontrar la probabilidad de que se elijan menos de (2 ) perros.
( dfrac {63} {1,001} + dfrac {315} {1,001} = dfrac {378} {1,001} )
Luego restamos esa probabilidad de (1 ) para encontrar la probabilidad de que se elijan al menos (2 ) perros.
(1− dfrac {378} {1,001} = dfrac {623} {1,001} )
Ejercicio ( PageIndex {5} )
Un niño selecciona aleatoriamente (3 ) chicles de un contenedor que contiene (4 ) chicles púrpuras, (8 ) chicles amarillos y (2 ) chicles verdes.
- Encuentre la probabilidad de que todos los (3 ) chicles seleccionados sean morados.
- Encuentre la probabilidad de que no se seleccionen chicles amarillos.
- Encuentre la probabilidad de que al menos (1 ) chicle amarillo esté seleccionado.
- Respuesta
-
( dfrac {1} {91} )
- Respuesta
-
( dfrac {5} {91} )
- Respuesta
-
( dfrac {86} {91} )
Medios
Acceda a estos recursos en línea para obtener instrucción adicional y practicar con probabilidad.
Visite este sitio web para preguntas de práctica adicionales de Learningpod.
