
Raíces cuadradas aproximadas con una calculadora
Existen métodos matemáticos para aproximar raíces cuadradas, pero es mucho más conveniente usar una calculadora para encontrar raíces cuadradas. Busque la tecla ( sqrt { text {}} ) o ( sqrt {x} ) en su calculadora. Deberá usar esta tecla para aproximar raíces cuadradas. Cuando usa su calculadora para encontrar la raíz cuadrada de un número que no es un cuadrado perfecto, la respuesta que ve no es el número exacto. Es una aproximación al número de dígitos que se muestran en la pantalla de su calculadora. El símbolo para una aproximación es ≈ y se lee aproximadamente .
Suponga que su calculadora tiene una pantalla de 10 dígitos. Usarlo para encontrar la raíz cuadrada de 5 dará 2.236067977. Esta es la raíz cuadrada aproximada de 5. Cuando informamos la respuesta, debemos usar el signo “aproximadamente igual a” en lugar de un signo igual.
$$ sqrt {5} aprox 2.236067978 $$
Rara vez usará esta cantidad de dígitos para aplicaciones en álgebra. Entonces, si quisiera redondear ( sqrt {5} ) a dos decimales, escribiría
$$ sqrt {5} aprox 2.24 $$
¿Cómo sabemos que estos valores son aproximaciones y no los valores exactos? Mira lo que sucede cuando los cuadramos.
$$ begin {split} 2.236067978 ^ {2} & = 5.000000002 \ 2.24 ^ {2} & = 5.0176 end {split} $$
Los cuadrados están cercanos, pero no exactamente iguales, a 5.
Ejemplo ( PageIndex {6} ):
Redondea ( sqrt {17} ) a dos decimales usando una calculadora.
Solución
| Usa la calculadora de raíz cuadrada. | 4.123105626 |
| Redondear a dos decimales. | 4.12 |
| $$ sqrt {17} aprox 4.12 $$ |
Ejercicio ( PageIndex {11} ):
Redondea ( sqrt {11} ) a dos decimales.
- Respuesta
-
( aprox 3.32 )
Ejercicio ( PageIndex {12} ):
Redondea ( sqrt {13} ) a dos decimales
- Respuesta
-
( aprox 3.61 )
Simplificar expresiones variables con raíces cuadradas
Las expresiones con raíz cuadrada que hemos visto hasta ahora no han tenido ninguna variable. ¿Qué sucede cuando tenemos que encontrar una raíz cuadrada de una expresión variable?
Considera ( sqrt {9x ^ {2}} ), donde x ≥ 0. ¿Puedes pensar en una expresión cuyo cuadrado sea 9x 2 ?
$$ begin {split} (?) ^ {2} & = 9x ^ {2} \ (3x) ^ {2} & = 9x ^ {2} \ so ; sqrt {9x ^ {2}} & = 3x end {split} $$
Cuando usamos una variable en una expresión de raíz cuadrada, para nuestro trabajo, asumiremos que la variable representa un número no negativo. En cada ejemplo y ejercicio que sigue, cada variable en una expresión de raíz cuadrada es mayor o igual que cero.
Ejemplo ( PageIndex {7} ):
Simplificar: x 2 .
Solución
Piensa en lo que tendríamos que cuadrar para obtener x 2 . Algebraicamente, (?) 2 = x 2
Ejercicio ( PageIndex {13} ):
Simplifique: ( sqrt {y ^ {2}} ).
- Respuesta
-
(y )
Ejercicio ( PageIndex {14} ):
Simplifique: ( sqrt {m ^ {2}} ).
- Respuesta
-
(m )
Ejemplo ( PageIndex {8} ):
Simplifique: ( sqrt {16x ^ {2}} ).
Solución
Ejercicio ( PageIndex {15} ):
Simplifique: ( sqrt {64x ^ {2}} ).
- Respuesta
-
(8x )
Ejercicio ( PageIndex {16} ):
Simplifique: ( sqrt {169y ^ {2}} ).
- Respuesta
-
(13 años )
Ejemplo ( PageIndex {9} ):
Simplifique: (- sqrt {81y ^ {2}} ).
Solución
Ejercicio ( PageIndex {17} ):
Simplifique: (- sqrt {121y ^ {2}} ).
- Respuesta
-
(- 11 años )
Ejercicio ( PageIndex {18} ):
Simplifique: (- sqrt {100p ^ {2}} ).
- Respuesta
-
(- 10p )
Ejemplo ( PageIndex {10} ):
Simplifique: ( sqrt {36x ^ {2} y ^ {2}} ).
Solución
| Desde (6xy) 2 = 36x 2 y 2 | 6xy |
Ejercicio ( PageIndex {19} ):
Simplifique: ( sqrt {100a ^ {2} b ^ {2}} ).
- Respuesta
-
(10ab )
Ejercicio ( PageIndex {20} ):
Simplifique: ( sqrt {225m ^ {2} n ^ {2}} ).
- Respuesta
-
(10mn )
Usar raíces cuadradas en aplicaciones
A medida que avanzas en tus cursos universitarios, encontrarás varias aplicaciones de raíces cuadradas. Una vez más, si usamos nuestra estrategia para aplicaciones, ¡nos dará un plan para encontrar la respuesta!
CÓMO: USAR UNA ESTRATEGIA PARA APLICACIONES CON RAÍCES CUADRADAS
Paso 1. Identifica lo que se te pide que encuentres.
Paso 2. Escribe una frase que proporcione la información para encontrarla.
Paso 3. Traduce la frase a una expresión.
Paso 4. Simplifica la expresión.
Paso 5. Escribe una oración completa que responda la pregunta.
Raíces cuadradas y área
Hemos resuelto aplicaciones con área antes. Si se nos diera la longitud de los lados de un cuadrado, podríamos encontrar su área cuadrando la longitud de sus lados. Ahora podemos encontrar la longitud de los lados de un cuadrado si se nos da el área, al encontrar la raíz cuadrada del área.
Si el área del cuadrado es A unidades cuadradas, la longitud de un lado es A unidades. Consulte la Tabla ( PageIndex {1} ).
| Área (unidades cuadradas) | Longitud del lado (unidades) |
|---|---|
| 9 | $$ sqrt {9} = 3 $$ |
| 144 | $$ sqrt {144} = 12 $$ |
| A | $$ sqrt {A} $$ |
Ejemplo ( PageIndex {11} ):
Mike y Lychelle quieren hacer un patio cuadrado. Tienen suficiente concreto para un área de 200 pies cuadrados. A la décima de pie más cercana, ¿cuánto tiempo puede ser un lado de su patio cuadrado?
Solución
Sabemos que el área del cuadrado es de 200 pies cuadrados y queremos encontrar la longitud del lado. Si el área del cuadrado es A unidades cuadradas, la longitud de un lado es ( sqrt {A} ) unidades.
| ¿Qué se te pide encontrar? | La longitud de cada lado de un patio cuadrado |
| Escribe una frase. | La longitud de un lado |
| Traducir a una expresión. | $$ sqrt {A} $$ |
| Evalúe ( sqrt {A} ) cuando A = 200. | $$ sqrt {200} $$ |
| Usa tu calculadora. | 14,142135 … |
| Redondea a un decimal. | 14.1 pies |
| Escribe una oración. | Cada lado del patio debe tener 14.1 pies. |
Ejercicio ( PageIndex {21} ):
Katie quiere plantar un césped cuadrado en su patio delantero. Ella tiene suficiente césped para cubrir un área de 370 pies cuadrados. A la décima de pie más cercana, ¿cuánto puede ser un lado de su césped cuadrado?
- Respuesta
-
19,2 pies
Ejercicio ( PageIndex {22} ):
Sergio quiere hacer un mosaico cuadrado como incrustación para una mesa que está construyendo. Tiene suficiente mosaico para cubrir un área de 2704 centímetros cuadrados. ¿Cuánto tiempo puede ser un lado de su mosaico?
- Respuesta
-
52 centímetros
Raíces cuadradas y gravedad
Otra aplicación de raíces cuadradas implica la gravedad. En la Tierra, si un objeto se cae desde una altura de h pies, el tiempo en segundos que tomará llegar al suelo se determina evaluando la expresión ( dfrac { sqrt {h}} {4} ). Por ejemplo, si un objeto se cae desde una altura de 64 pies, podemos encontrar el tiempo que lleva llegar al suelo evaluando ( dfrac { sqrt {64}} {4} ).
| Saca la raíz cuadrada de 64. | $$ dfrac {8} {4} $$ |
| Simplifica la fracción. | 2 |
Tomaría 2 segundos para que un objeto caído desde una altura de 64 pies alcance el suelo.
Ejemplo ( PageIndex {12} ):
Christy dejó caer sus gafas de sol desde un puente a 400 pies sobre un río. ¿Cuántos segundos tardan las gafas de sol en llegar al río?
Solución
| ¿Qué se te pide encontrar? | El número de segundos que tardan las gafas de sol en llegar al río |
| Escribe una frase. | El tiempo que tomará llegar al río |
| Traducir a una expresión. | $$ dfrac { sqrt {h}} {4} $$ |
| Evalúe ( dfrac { sqrt {h}} {4} ) cuando h = 400. | $$ dfrac { sqrt {400}} {4} $$ |
| Encuentra la raíz cuadrada de 400. | 14,142135 … |
| Simplifica. | 14.1 pies |
| Escribe una oración. | Cada lado del patio debe tener 14.1 pies. |
Ejercicio ( PageIndex {23} ):
Un helicóptero lanza un paquete de rescate desde una altura de 1296 pies. ¿Cuántos segundos tarda el paquete en llegar al suelo?
- Respuesta
-
9 segundos
Ejercicio ( PageIndex {24} ):
Un limpiador de ventanas deja caer una escobilla de goma desde una plataforma a 196 pies sobre la acera. ¿Cuántos segundos le toma a la escobilla de goma llegar a la acera?
- Respuesta
-
3,5 segundos
Raíces cuadradas e investigaciones de accidentes
Los oficiales de policía que investigan accidentes automovilísticos miden la longitud de las marcas de deslizamiento en el pavimento. Luego usan raíces cuadradas para determinar la velocidad, en millas por hora, iba un automóvil antes de aplicar los frenos. Según algunas fórmulas, si la longitud de las marcas de deslizamiento es d pies, entonces la velocidad del automóvil se puede encontrar evaluando ( sqrt {24d} ).
Ejemplo ( PageIndex {13} ):
Después de un accidente automovilístico, las marcas de derrape para un automóvil midieron 190 pies. A la décima más cercana, ¿cuál era la velocidad del automóvil (en mph) antes de aplicar los frenos?
Solución
| ¿Qué se te pide encontrar? | La velocidad del automóvil antes de que se aplicaran los frenos |
| Escribe una frase. | La velocidad del automóvil |
| Traducir a una expresión. | $$ sqrt {24d} $$ |
| Evalúe ( sqrt {24d} ) cuando d = 190. | $$ sqrt {24 cdot 190} $$ |
| Multiplica. | $$ sqrt {4,560} $$ |
| Usa tu calculadora. | 67,527772 … |
| Redondear a décimas. | 67,5 |
| Escribe una oración. | La velocidad del automóvil era de aproximadamente 67.5 millas por hora. |
Ejercicio ( PageIndex {25} ):
Un investigador de accidentes midió las marcas de derrape de un automóvil y descubrió que su longitud era de 76 pies. A la décima más cercana, ¿cuál era la velocidad del automóvil antes de aplicar los frenos?
- Respuesta
-
42.7 mph
Ejercicio ( PageIndex {26} ):
Las marcas de derrape de un vehículo involucrado en un accidente tenían 122 pies de largo. A la décima más cercana, ¿qué tan rápido había estado yendo el vehículo antes de aplicar los frenos?
- Respuesta
-
54,1 mph
La práctica hace la perfección
Simplificar expresiones con raíces cuadradas
En los siguientes ejercicios, simplifica.
- ( sqrt {36} )
- ( sqrt {4} )
- ( sqrt {64} )
- ( sqrt {144} )
- (- sqrt {4} )
- (- sqrt {100} )
- (- sqrt {1} )
- (- sqrt {121} )
- ( sqrt {-121} )
- ( sqrt {-36} )
- ( sqrt {-9} )
- ( sqrt {-49} )
- ( sqrt {9 + 16} )
- ( sqrt {25 + 144} )
- ( sqrt {9} + sqrt {16} )
- ( sqrt {25} + sqrt {144} )
Estimación de raíces cuadradas
En los siguientes ejercicios, estima cada raíz cuadrada entre dos números enteros consecutivos.
- ( sqrt {70} )
- ( sqrt {5} )
- ( sqrt {200} )
- ( sqrt {172} )
Raíces cuadradas aproximadas con una calculadora
En los siguientes ejercicios, usa una calculadora para aproximar cada raíz cuadrada y redondear a dos decimales.
- ( sqrt {19} )
- ( sqrt {21} )
- ( sqrt {53} )
- ( sqrt {47} )
Simplificar expresiones variables con raíces cuadradas
En los siguientes ejercicios, simplifica. (Suponga que todas las variables son mayores o iguales que cero).
- ( sqrt {y ^ {2}} )
- ( sqrt {b ^ {2}} )
- ( sqrt {49x ^ {2}} )
- ( sqrt {100y ^ {2}} )
- (- sqrt {64a ^ {2}} )
- (- sqrt {25x ^ {2}} )
- ( sqrt {144x ^ {2} y ^ {2}} )
- ( sqrt {196a ^ {2} b ^ {2}} )
Usar raíces cuadradas en aplicaciones
En los siguientes ejercicios, resuelve. Redondea a un decimal.
- Paisajismo Reed quiere tener una parcela cuadrada en su patio trasero. Tiene suficiente abono para cubrir un área de 75 pies cuadrados. ¿Cuánto tiempo puede ser un lado de su jardín?
- Paisajismo Vince quiere hacer un patio cuadrado en su patio. Tiene suficiente concreto para pavimentar un área de 130 pies cuadrados. ¿Cuánto tiempo puede ser un lado de su patio?
- Gravedad Un avión dejó caer una bengala desde una altura de 1.024 pies sobre un lago. ¿Cuántos segundos le tomó a la bengala alcanzar el agua?
- Gravedad Un ala delta dejó caer su teléfono celular desde una altura de 350 pies. ¿Cuántos segundos le tomó al teléfono celular llegar al suelo?
- Gravedad Un trabajador de la construcción dejó caer un martillo mientras construía la pasarela del Gran Cañón, a 4.000 pies sobre el río Colorado. ¿Cuántos segundos le tomó al martillo llegar al río?
- Investigación de accidente Las marcas de derrape de un automóvil involucrado en un accidente midieron 54 pies. ¿Cuál era la velocidad del automóvil antes de aplicar los frenos?
- Investigación de accidente Las marcas de derrape de un automóvil involucrado en un accidente midieron 216 pies. ¿Cuál era la velocidad del automóvil antes de aplicar los frenos?
- Investigación de accidente Un investigador de accidentes midió las marcas de deslizamiento de uno de los vehículos involucrados en un accidente. La longitud de las marcas de deslizamiento fue de 175 pies. ¿Cuál era la velocidad del vehículo antes de aplicar los frenos?
- Investigación de accidente Un investigador de accidentes midió las marcas de deslizamiento de uno de los vehículos involucrados en un accidente. La longitud de las marcas de deslizamiento fue de 117 pies. ¿Cuál era la velocidad del vehículo antes de aplicar los frenos?
Matemáticas cotidianas
- Decoración Denise quiere instalar un acento cuadrado de azulejos de diseño en su nueva ducha. Puede darse el lujo de comprar 625 centímetros cuadrados de azulejos de diseño. ¿Cuánto tiempo puede ser un lado del acento?
- Decoración Morris quiere tener un mosaico cuadrado con incrustaciones en su nuevo patio. Su presupuesto permite 2.025 azulejos. Cada mosaico es cuadrado con un área de una pulgada cuadrada. ¿Cuánto tiempo puede ser un lado del mosaico?
Ejercicios de escritura
- ¿Por qué no hay un número real igual a ( sqrt {−64} )?
- ¿Cuál es la diferencia entre 9 2 y ( sqrt {9} )?
Autocomprobación
(a) Después de completar los ejercicios, use esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
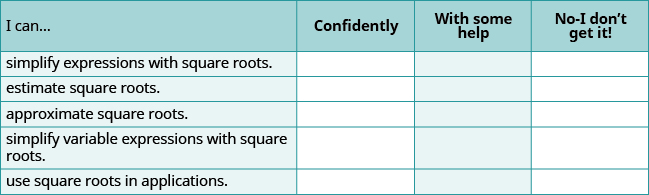
(b) En general, después de mirar la lista de verificación, ¿cree que está bien preparado para el próximo Capítulo? ¿Por qué o por qué no?
