
Una nueva panadería ofrece pasteles decorados para fiestas de cumpleaños infantiles y otras ocasiones especiales. La panadería quiere que el volumen de un pastel pequeño sea de 351 pulgadas cúbicas. El pastel tiene la forma de un sólido rectangular. Quieren que la longitud del pastel sea cuatro pulgadas más larga que el ancho del pastel y que la altura del pastel sea un tercio del ancho. ¿Cuáles deberían ser las dimensiones del molde para pasteles?
Este problema se puede resolver escribiendo una función cúbica y resolviendo una ecuación cúbica para el volumen del pastel. En esta sección, discutiremos una variedad de herramientas para escribir funciones polinómicas y resolver ecuaciones polinómicas.
Evaluación de un polinomio usando el teorema del resto
En la última sección, aprendimos cómo dividir polinomios. Ahora podemos usar la división polinomial para evaluar polinomios usando el Teorema del resto . Si el polinomio se divide por (x – k ), el resto se puede encontrar rápidamente evaluando la función polinomial en (k ), es decir, (f (k) ). Veamos la prueba del teorema.
Recuerde que el algoritmo de división establece que, dado un dividendo polinomial (f (x) ) y un divisor polinomial distinto de cero (d (x) ) donde el grado de (d (x) ) es menor o igual que el grado de (f (x) ), existen polinomios únicos (q (x) ) y (r (x) ) tales que
[f (x) = d (x) q (x) + r (x) nonumber ]
Si el divisor, (d (x) ), es (x − k ), esto toma la forma
[f (x) = (x − k) q (x) + r nonumber ]
Dado que el divisor (x − k )
es lineal, el resto será una constante, (r ). Y, si evaluamos esto para (x = k ), tenemos
[ begin {align *} f (k) & = (k − k) q (k) + r \ [4pt] & = 0 { cdot} q (k) + r \ [4pt ] & = r end {alinear *} ]
En otras palabras, (f (k) ) es el resto obtenido al dividir (f (x) ) por (x − k ).
El teorema del resto
Si un polinomio (f (x) ) se divide por (x − k ), el resto es el valor (f (k) ).
![]() Dada una función polinómica (f ), evalúa (f (x) ) en (x = k ) usando el Teorema del resto.
Dada una función polinómica (f ), evalúa (f (x) ) en (x = k ) usando el Teorema del resto.
- Usa la división sintética para dividir el polinomio por (x − k ).
- El resto es el valor (f (k) ).
Ejemplo ( PageIndex {1} ): Uso del teorema del resto para evaluar un polinomio
Usa el teorema del resto para evaluar (f (x) = 6x ^ 4 − x ^ 3−15x ^ 2 + 2x − 7 ) en (x = 2 ).
Solución
Para encontrar el resto usando el Teorema del resto, usa la división sintética para dividir el polinomio por (x − 2 ).
[2 begin {array} {| ccccc} ; 6 y −1 y −15 y 2 y −7 \ text {} y 12 y 22 y 14 y 32 \ hline end {array} \ begin {array} {ccccc} 6 y 11 y ; 7 & ; ; 16 & ; ; 25 end {array} ]
El resto es 25. Por lo tanto, (f (2) = 25 ).
Análisis
Podemos verificar nuestra respuesta evaluando (f (2) ).
[ begin {align *} f (x) & = 6x ^ 4 − x ^ 3−15x ^ 2 + 2x − 7 \ f (2) & = 6 (2) ^ 4− (2) ^ 3−15 (2) ^ 2 + 2 (2) −7 \ & = 25 end {align *} ]
Ejercicio ( PageIndex {1} )
ve el Teorema del resto para evaluar (f (x) = 2x ^ 5−3x ^ 4−9x ^ 3 + 8x ^ 2 + 2 ) en (x = −3 ).
- Respuesta
-
(f (−3) = – 412 )
Usando el teorema del factor para resolver una ecuación polinómica
El teorema del factor es otro teorema que nos ayuda a analizar ecuaciones polinómicas. Nos dice cómo los ceros de un polinomio están relacionados con los factores. Recordemos que el algoritmo de división.
[f (x) = (x − k) q (x) + r ]
Si (k ) es un cero, entonces el resto (r ) es (f (k) = 0 ) y (f (x) = (x − k) q (x) + 0 ) o (f (x) = (x − k) q (x) ).
Aviso, escrito en esta forma, (x − k ) es un factor de (f (x) ). Podemos concluir si (k ) es un cero de (f (x) ), entonces (x − k ) es un factor de (f (x) ).
Del mismo modo, si (x − k ) es un factor de (f (x) ), entonces el resto del Algoritmo de división (f (x) = (x − k) q (x) + r ) es (0 ). Esto nos dice que (k ) es un cero.
Este par de implicaciones es el teorema del factor. Como veremos pronto, un polinomio de grado (n ) en el sistema de números complejos tendrá (n ) ceros. Podemos usar el Teorema del factor para factorizar completamente un polinomio en el producto de factores (n ). Una vez que el polinomio se ha factorizado por completo, podemos determinar fácilmente los ceros del polinomio.
EL TEOREMA DEL FACTOR
Según el teorema del factor, (k ) es un cero de (f (x) ) si y solo si ((x − k) ) es un factor de (f (x) )
Cómo: dado un factor y un polinomio de tercer grado, usa el Teorema del factor para factorizar el polinomio
- Usa la división sintética para dividir el polinomio por ((x − k) ).
- Confirme que el resto es (0 ).
- Escribe el polinomio como el producto de ((x − k) ) y el cociente cuadrático.
- Si es posible, factorizar la cuadrática.
- Escribe el polinomio como el producto de factores.
Ejemplo ( PageIndex {2} ): Uso del teorema del factor para resolver una ecuación polinómica
Demuestre que ((x + 2) ) es un factor de (x ^ 3−6x ^ 2 − x + 30 ). Encuentra los factores restantes. Use los factores para determinar los ceros del polinomio .
Solución
Podemos usar la división sintética para mostrar que ((x + 2) ) es un factor del polinomio.
[-2 begin {array} {| cccc} ; 1 & −6 & −1 & 30 \ text {} & -2 & 16 & -30 \ hline end {array} \ begin {array} {cccc} 1 & -8 & ; 15 & ; ; 0 end {array} ]
El resto es cero, entonces ((x + 2) ) es un factor del polinomio. Podemos usar el algoritmo de división para escribir el polinomio como el producto del divisor y el cociente:
[(x + 2) (x ^ 2−8x + 15) ]Podemos factorizar el factor cuadrático para escribir el polinomio como
[(x + 2) (x − 3) (x − 5) ]Según el teorema del factor, los ceros de (x ^ 3−6x ^ 2 − x + 30 ) son –2, 3 y 5.
Ejercicio ( PageIndex {2} )
Usa el teorema del factor para encontrar los ceros de (f (x) = x ^ 3 + 4x ^ 2−4x − 16 ) dado que ((x − 2) ) es un factor del polinomio.
- Respuesta
-
Los ceros son 2, –2 y –4.
Usando el teorema de Rational Zero para encontrar ceros racionales
Otro uso para el teorema del resto es probar si un número racional es cero para un polinomio dado. Pero primero necesitamos un grupo de números racionales para probar. El Rational Zero Theorem nos ayuda a reducir el número de ceros racionales posibles usando la razón de los factores del término constante y los factores del coeficiente principal del polinomio
Considere una función cuadrática con dos ceros, (x = frac {2} {5} ) y (x = frac {3} {4} ). Por el teorema del factor, estos ceros tienen factores asociados con ellos. Pongamos cada factor igual a 0, y luego construyamos la función cuadrática original en ausencia de su factor de estiramiento.

Observe que dos de los factores del término constante, 6, son los dos numeradores de las raíces racionales originales: 2 y 3. De manera similar, dos de los factores del coeficiente principal, 20, son los dos denominadores del original Raíces racionales: 5 y 4.
Podemos inferir que los numeradores de las raíces racionales siempre serán factores del término constante y los denominadores serán factores del coeficiente principal. Esta es la esencia del teorema racional racional; Es un medio para darnos un grupo de posibles ceros racionales.
EL TEOREMA CERO RACIONAL
El teorema del cero racional establece que, si el polinomio (f (x) = a_nx ^ n + a_ {n − 1} x ^ {n − 1} + … + a_1x + a_0 ) tiene coeficientes enteros , entonces cada cero racional de (f (x) ) tiene la forma ( frac {p} {q} ) donde (p ) es un factor del término constante (a_0 ) y ( q ) es un factor del coeficiente principal (a_n ).
Cuando el coeficiente principal es 1, los posibles ceros racionales son los factores del término constante.
Cómo: Dada una función polinómica (f (x) ), usa el Teorema del cero racional para encontrar ceros racionales.
- Determine todos los factores del término constante y todos los factores del coeficiente principal.
- Determine todos los valores posibles de ( dfrac {p} {q} ), donde (p ) es un factor del término constante y (q ) es un factor del coeficiente principal. Asegúrese de incluir candidatos tanto positivos como negativos.
- Determine qué ceros posibles son ceros reales evaluando cada caso de (f ( frac {p} {q}) ).
Ejemplo ( PageIndex {3} ): Listado de todos los ceros racionales posibles
Enumere todos los ceros racionales posibles de (f (x) = 2x ^ 4−5x ^ 3 + x ^ 2−4 ).
Solución:
Los únicos ceros racionales posibles de (f (x) ) son los cocientes de los factores del último término, –4, y los factores del coeficiente principal, 2.
El término constante es –4; Los factores de –4 son (p = ± 1, ± 2, ± 4 ).
El coeficiente principal es 2; los factores de 2 son (q = ± 1, ± 2 ).
Si alguno de los cuatro ceros reales son ceros racionales, serán uno de los siguientes factores de –4 dividido por uno de los factores de 2.
[ dfrac {p} {q} = ± dfrac {1} {1}, ± dfrac {1} {2} ; ; ; ; ; ; frac {p} {q} = ± dfrac {2} {1}, ± dfrac {2} {2} ; ; ; ; ; ; dfrac {p} {q} = ± dfrac {4} {1}, ± dfrac {4} {2} nonumber ]Tenga en cuenta que ( frac {2} {2} = 1 ) y ( frac {4} {2} = 2 ), que ya se han enumerado. Entonces podemos acortar nuestra lista.
[ dfrac {p} {q} = dfrac { text {Factores de la última}} { text {Factores de la primera}} = ± 1, ± 2, ± 4, ± dfrac { 1} {2} nonumber ]
Ejemplo ( PageIndex {4} ): Uso del teorema de Rational Zero para encontrar ceros racionales
Usa el teorema del cero racional para encontrar los ceros racionales de (f (x) = 2x ^ 3 + x ^ 2−4x + 1 ).
Solución:
El teorema del cero racional nos dice que si ( frac {p} {q} ) es un cero de (f (x) ), entonces (p ) es un factor de 1 y ( q ) es un factor de 2.
[ begin {align *} dfrac {p} {q} = dfrac {factor space of space constant space term} {factor space of space Leading space coefficient} \ [4pt ] & = dfrac {factor espacio de espacio 1} {factor espacio de espacio 2} end {align *} ]
Los factores de 1 son ± 1 y los factores de 2 son ± 1 y ± 2. Los valores posibles para ( frac {p} {q} ) son ± 1 y (± frac {1} {2} ). Estos son los posibles ceros racionales para la función. Podemos determinar cuáles de los ceros posibles son ceros reales sustituyendo estos valores por (x ) en (f (x) ).
[f (−1) = 2 {(- 1)} ^ 3 + {(- 1)} ^ 2−4 (−1) + 1 = 4 ]
[f (1) = 1 {(1)} ^ 3 + {(1)} ^ 2−4 (1) + 1 = 0 ][f (- dfrac {1} {2}) = 2 {(- dfrac {1} {2})} ^ 3 + {(- dfrac {1} {2})} ^ 2 −4 (- dfrac {1} {2}) + 1 = 3 ]
[f ( dfrac {1} {2}) = 2 {( dfrac {1} {2})} ^ 3 + {( dfrac {1} {2})} ^ 2−4 ( dfrac { 1} {2}) + 1 = – dfrac {1} {2} ]De ellos, (- 1 ), (- dfrac {1} {2} ) y ( dfrac {1} {2} ) no son ceros de (f (x) ). 1 es el único cero racional de (f (x) ).
Ejercicio ( PageIndex {3} )
Usa el teorema del cero racional para encontrar los ceros racionales de (f (x) = x ^ 3−5x ^ 2 + 2x + 1 ).
- Respuesta
-
No hay ceros racionales.
Encontrar los ceros de las funciones polinomiales
El teorema del cero racional nos ayuda a reducir la lista de posibles ceros racionales para una función polinómica. Una vez que hayamos hecho esto, podemos usar división sintética repetidamente para determinar todos los ceros de una función polinómica.
Cómo: Dada una función polinómica (f ), usa la división sintética para encontrar sus ceros.
- Utilice el teorema del cero racional para enumerar todos los ceros racionales posibles de la función.
- Use la división sintética para evaluar un posible cero dado dividiendo sintéticamente al candidato en el polinomio. Si el resto es 0, el candidato es un cero. Si el resto no es cero, descarte al candidato.
- Repita el paso dos usando el cociente encontrado con la división sintética. Si es posible, continúe hasta que el cociente sea cuadrático.
- Encuentra los ceros de la función cuadrática. Dos posibles métodos para resolver las cuadráticas son factorizar y usar la fórmula cuadrática.
Ejemplo ( PageIndex {5} ): Encontrar los ceros de una función polinómica con ceros reales repetidos
Encuentra los ceros de (f (x) = 4x ^ 3−3x − 1 ).
Solución:
El teorema del cero racional nos dice que si ( dfrac {p} {q} ) es un cero de (f (x) ), entonces (p ) es un factor de –1 y (q ) es un factor de 4.
[ begin {align *} dfrac {p} {q} = dfrac {factor space of space constant space term} {factor space of space Leading space coefficient} \ [4pt ] = dfrac {factor espacio de espacio -1} {factor espacio de espacio 4} end {align *} ]
Los factores de –1 son ± 1 y los factores de 4 son ± 1, ± 2 y ± 4. Los valores posibles para ( dfrac {p} {q} ) son (± 1 ), (± dfrac {1} {2} ) y (± dfrac {1} {4} ). Estos son los posibles ceros racionales para la función. Utilizaremos la división sintética para evaluar cada cero posible hasta que encontremos uno que dé un resto de 0. Comencemos con 1.
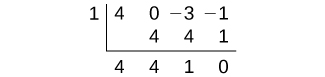
La división entre ((x − 1) ) da un resto de 0, por lo que 1 es un cero de la función. El polinomio se puede escribir como
[(x − 1) (4x ^ 2 + 4x + 1) nonumber ]
El cuadrático es un cuadrado perfecto. (f (x) ) se puede escribir como
[(x − 1) {(2x + 1)} ^ 2 nonumber ]
Ya sabemos que 1 es un cero. El otro cero tendrá una multiplicidad de 2 porque el factor es cuadrado. Para encontrar el otro cero, podemos establecer el factor igual a 0.
[ begin {align *} 2x + 1 = 0 \ [4pt] x & = – dfrac {1} {2} end {align *} ]
Los ceros de la función son 1 y (- frac {1} {2} ) con multiplicidad 2.
AnálisisObserve el gráfico de la función (f ) en la Figura ( PageIndex {1} ). Observe que, en (x = −0.5 ), el gráfico rebota en el eje x, lo que indica la multiplicidad par (2,4,6 …) para el cero −0.5. En (x = 1 ), el gráfico cruza el eje x, indicando la multiplicidad impar (1,3,5 …) para el cero (x = 1 ).
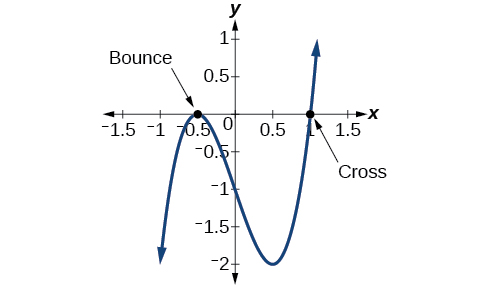
Usando el teorema fundamental del álgebra
Ahora que podemos encontrar ceros racionales para una función polinómica, veremos un teorema que analiza el número de ceros complejos de una función polinómica. El Teorema fundamental del álgebra nos dice que cada función polinómica tiene al menos un cero complejo. Este teorema forma la base para resolver ecuaciones polinómicas.
Supongamos que (f ) es una función polinómica de grado cuatro y (f (x) = 0 ). El teorema fundamental del álgebra establece que hay al menos una solución compleja, llámela (c_1 ). Por el teorema del factor, podemos escribir (f (x) ) como un producto de (x − c_1 ) y un cociente polinomial. Como (x − c_1 ) es lineal, el cociente polinomial será de grado tres. Ahora aplicamos el teorema fundamental del álgebra al cociente polinomial de tercer grado. Tendrá al menos un cero complejo, llámelo (c_2 ). Entonces, podemos escribir el cociente polinomial como un producto de (x − c_2 ) y un nuevo cociente polinomial de grado dos. Continúe aplicando el Teorema fundamental del álgebra hasta que se encuentren todos los ceros. Habrá cuatro de ellos y cada uno producirá un factor de (f (x) ).
EL TEOREMA FUNDAMENTAL DEL ÁLGEBRA
El Teorema fundamental del álgebra establece que, si (f (x) ) es un polinomio de grado (n> 0 ), entonces (f ( x) ) tiene al menos un cero complejo.
Podemos usar este teorema para argumentar que, si (f (x) ) es un polinomio de grado (n> 0 ), y a es un número real distinto de cero, entonces (f (x ) ) tiene exactamente (n ) factores lineales
[f (x) = a (x − c_1) (x − c_2) … (x − c_n) ]donde (c_1, c_2 ), …, (c_n ) son números complejos. Por lo tanto, (f (x) ) tiene raíces (n ) si permitimos multiplicidades.
P y R: ¿Cada polinomio tiene al menos un cero imaginario?
No. Los números reales son un subconjunto de números complejos, pero no al revés. Un número complejo no es necesariamente imaginario. Los números reales también son números complejos.
Ejemplo ( PageIndex {6} ): Encontrar los ceros de una función polinómica con ceros complejos
Encuentra los ceros de (f (x) = 3x ^ 3 + 9x ^ 2 + x + 3 ).
Solución:
El teorema del cero racional nos dice que si ( frac {p} {q} ) es un cero de (f (x) ), entonces (p ) es un factor de 3 y ( q ) es un factor de 3.
[ begin {align *} dfrac {p} {q} = dfrac {factor space of space constant space term} {factor space of space Leading space coefficient} \ [4pt ] & = dfrac {factor espacio de espacio 3} {factor espacio de espacio 3} end {align *} ]
Los factores de 3 son ± 1 y ± 3. Los valores posibles para ( dfrac {p} {q} ), y por lo tanto los posibles ceros racionales para la función, son ± 3, ± 1 y (± dfrac {1} {3} ). Usaremos la división sintética para evaluar cada cero posible hasta que encontremos uno que dé un resto de 0. Comencemos con –3.
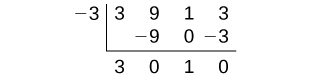
Dividir entre ((x + 3) ) da un resto de 0, entonces –3 es un cero de la función. El polinomio se puede escribir como
[(x + 3) (3x ^ 2 + 1) nonumber ]Entonces podemos establecer la cuadrática igual a 0 y resolver para encontrar los otros ceros de la función.
[ begin {align *} 3x ^ 2 + 1 = 0 \ [4pt] x ^ 2 & = – dfrac {1} {3} \ [4pt] x & = ± – sqrt { dfrac {1 } {3}} \ [4pt] & = ± dfrac {i sqrt {3}} {3} end {align *} ]Los ceros de (f (x) ) son (- 3 ) y (± dfrac {i sqrt {3}} {3} ).
Mire la gráfica de la función (f ) en la Figura ( PageIndex {2} ). Observe que, en (x = −3 ), el gráfico cruza el eje x, lo que indica una multiplicidad impar (1) para el cero (x = –3 ). También tenga en cuenta la presencia de los dos puntos de inflexión. Esto significa que, dado que hay un polinomio de grado (3 ^ {rd} ), estamos viendo el número máximo de puntos de inflexión. Entonces, el comportamiento final de aumentar sin limitar a la derecha y disminuir sin limitar a la izquierda continuará. Por lo tanto, se muestran todas las intersecciones en x para la función. Entonces, o la multiplicidad de (x = −3 ) es 1 y hay dos soluciones complejas, que es lo que encontramos, o la multiplicidad en (x = −3 ) es tres. De cualquier manera, nuestro resultado es correcto.
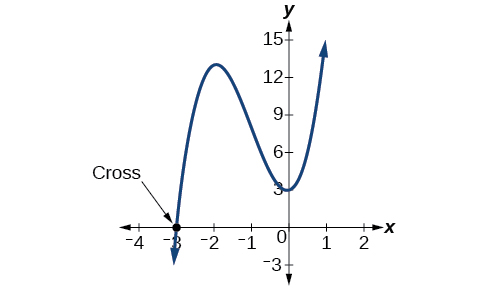
![]() ( PageIndex {4} )
( PageIndex {4} )
Encuentra los ceros de (f (x) = 2x ^ 3 + 5x ^ 2−11x + 4 ).
Solución:
Los ceros son (- 4 ), ( frac {1} {2} ) y (1 ).
Usando el teorema de factorización lineal para encontrar polinomios con ceros dados
Una implicación vital del Teorema fundamental del álgebra , como dijimos anteriormente, es que una función polinomial de grado n tendrá (n ) ceros en el conjunto de números complejos, si permitimos para multiplicidades Esto significa que podemos factorizar la función polinómica en factores (n ). El teorema de factorización lineal nos dice que una función polinomial tendrá el mismo número de factores que su grado, y que cada factor tendrá la forma ((x − c) ), donde c es un Número complejo.
Sea (f ) una función polinómica con coeficientes reales, y supongamos que (a + bi ), (b ≠ 0 ), es un cero de (f (x) ). Entonces, por el teorema del factor, (x− (a + bi) ) es un factor de (f (x) ). Para que (f ) tenga coeficientes reales, (x− (a − bi) ) también debe ser un factor de (f (x) ). Esto es cierto porque cualquier factor que no sea (x− (a − bi) ), cuando se multiplica por (x− (a + bi) ), dejará componentes imaginarios en el producto. Solo la multiplicación con pares conjugados eliminará las partes imaginarias y dará como resultado coeficientes reales. En otras palabras, si una función polinómica (f ) con coeficientes reales tiene un cero complejo (a + bi ), entonces el conjugado complejo (a − bi ) también debe ser un cero de (f (x ) ). Esto se llama Teorema del conjugado complejo .
Una nota general: TEOREMA CONJUGADO COMPLEJO
Según el teorema de factorización lineal, una función polinomial tendrá el mismo número de factores que su grado, y cada factor tendrá la forma ((x − c) ), donde (c ) es un Número complejo.
Si la función polinómica (f ) tiene coeficientes reales y un cero complejo en la forma (a + bi ), entonces el conjugado complejo del cero, (a − bi ), también es un cero .
Cómo
Dados los ceros de una función polinómica (f ) y un punto ((c, f (c)) ) en la gráfica de (f ), use el Teorema de factorización lineal para encontrar La función polinómica.
- Usa los ceros para construir los factores lineales del polinomio.
- Multiplica los factores lineales para expandir el polinomio.
- Sustituya ((c, f (c)) ) en la función para determinar el coeficiente principal.
- Simplificar.
Ejemplo ( PageIndex {7} ): Uso del teorema de factorización lineal para encontrar un polinomio con ceros dados
Encuentre un polinomio de cuarto grado con coeficientes reales que tenga ceros de (- 3 ), (2 ), (i ), de modo que (f (−2) = 100 ).
Solución:
Debido a que (x = i ) es un cero, por el teorema del conjugado complejo (x = –i ) también es un cero. El polinomio debe tener factores de ((x + 3), (x − 2), (x − i) ) y ((x + i) ). Como estamos buscando un polinomio de grado 4 y ahora tenemos cuatro ceros, tenemos los cuatro factores. Comencemos multiplicando estos factores.
[ begin {align} f (x) & = a (x + 3) (x − 2) (x − i) (x + i) \ f (x) & = a (x ^ 2 + x− 6) (x ^ 2 + 1) \ f (x) & = a (x ^ 4 + x ^ 3−5x ^ 2 + x − 6) end {align} ]Necesitamos encontrar (a ) para asegurar (f (–2) = 100 ). Sustituya (x = –2 ) y (f (-2) = 100 ) en (f (x) ).
[ begin {align} 100 = a ({(- 2)} ^ 4 + {(- 2)} ^ 3−5 {(- 2)} ^ 2 + (- 2) −6) \ 100 = a (−20) \ −5 = a end {align} ]Entonces, la función polinómica es
[f (x) = – 5 (x ^ 4 + x ^ 3−5x ^ 2 + x − 6) ]o
[f (x) = – 5x ^ 4−5x ^ 3 + 25x ^ 2−5x + 30 ]Encontramos que tanto (i ) como (- i ) eran ceros, pero solo era necesario dar uno de estos ceros. Si (i ) es un cero de un polinomio con coeficientes reales, entonces (- i ) también debe ser un cero del polinomio porque (- i ) es el conjugado complejo de (i ).
Preguntas y respuestas
Si se diera (2 + 3i ) como un cero de un polinomio con coeficientes reales, ¿ (2−3i ) también necesitaría ser un cero?
Sí. Cuando cualquier número complejo con un componente imaginario se da como un cero de un polinomio con coeficientes reales, el conjugado también debe ser un cero del polinomio.
![]() ( PageIndex {5} )
( PageIndex {5} )
Encuentre un polinomio de tercer grado con coeficientes reales que tenga ceros de (5 ) y (- 2i ) tal que (f (1) = 10 ).
Solución:
(f (x) = – frac {1} {2} x ^ 3 + frac {5} {2} x ^ 2−2x + 10 )
Usando la regla de signos de Descartes
Hay una forma directa de determinar los posibles números de ceros reales positivos y negativos para cualquier función polinómica. Si el polinomio está escrito en orden descendente, Regla de signos de Descartes nos informa de una relación entre el número de cambios de signo en (f (x) ) y el número de ceros reales positivos. Por ejemplo, la siguiente función polinómica tiene un cambio de signo.
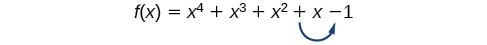
Esto nos dice que la función debe tener 1 cero real positivo.
Existe una relación similar entre el número de cambios de signo en (f (−x) ) y el número de ceros reales negativos.
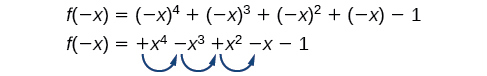
En este caso, (f (−x) ) tiene 3 cambios de signo. Esto nos dice que (f (x) ) podría tener 3 o 1 ceros reales negativos.
REGLA DE SEÑALES DE DESCARTES
De acuerdo con Regla de signos de Descartes , si dejamos que (f (x) = a_nx ^ n + a_ {n − 1} x ^ {n − 1} + … + a_1x + a_0 ) ser una función polinómica con coeficientes reales:
- El número de ceros reales positivos es igual al número de cambios de signo de (f (x) ) o es menor que el número de cambios de signo de un entero par.
- El número de ceros reales negativos es igual al número de cambios de signo de (f (−x) ) o es menor que el número de cambios de signo de un entero par.
Ejemplo ( PageIndex {8} ): Uso de la regla de signos de Descartes
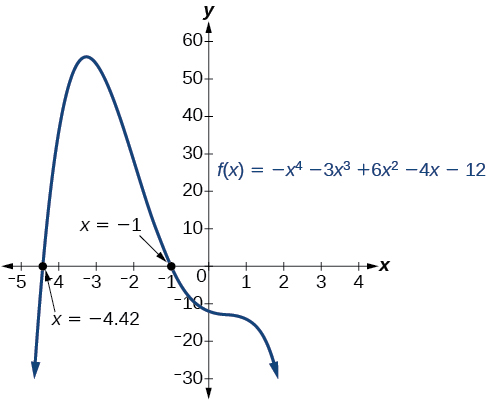
Use la regla de signos de Descartes para determinar los posibles números de ceros reales positivos y negativos para (f (x) = – x ^ 4−3x ^ 3 + 6x ^ 2−4x − 12 ).
Solución:
Comience por determinar el número de cambios de signos.
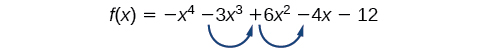
Hay dos cambios de signos, por lo que hay 2 o 0 raíces reales positivas. Luego, examinamos (f (−x) ) para determinar el número de raíces reales negativas.
[ begin {align} f (−x) & = – {(- x)} ^ 4−3 {(- x)} ^ 3 + 6 {(- x)} ^ 2−4 (−x) – 12 \ f (−x) & = −x ^ 4 + 3x ^ 3 + 6x ^ 2 + 4x − 12 end {align} ] 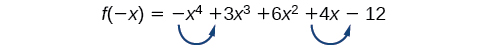
Nuevamente, hay dos cambios de signos, por lo que hay 2 o 0 raíces reales negativas.
Hay cuatro posibilidades, como podemos ver en la Tabla ( PageIndex {1} ).
| Ceros reales positivos | Ceros reales negativos | Ceros complejos | Ceros totales |
|---|---|---|---|
| 2 | 2 | 0 | 4 |
| 2 | 0 | 2 | 4 |
| 0 | 2 | 2 | 4 |
| 0 | 0 | 4 | 4 |
Podemos confirmar los números de raíces reales positivas y negativas examinando un gráfico de la función. Ver Figura ( PageIndex {3} ). Podemos ver en el gráfico que la función tiene 0 raíces reales positivas y 2 raíces reales negativas.
![]() ( PageIndex {6} )
( PageIndex {6} )
Use la regla de signos de Descartes para determinar los números máximos posibles de ceros reales positivos y negativos para (f (x) = 2x ^ 4−10x ^ 3 + 11x ^ 2−15x + 12 ). Use una gráfica para verificar los números de ceros reales positivos y negativos para la función.
Solución:
Debe haber 4, 2 o 0 raíces reales positivas y 0 raíces reales negativas. El gráfico muestra que hay 2 ceros reales positivos y 0 ceros reales negativos.
Resolviendo aplicaciones del mundo real
Ahora hemos introducido una variedad de herramientas para resolver ecuaciones polinómicas. Usemos estas herramientas para resolver el problema de la panadería desde el comienzo de la sección.
Ejemplo ( PageIndex {9} )
Una nueva panadería ofrece pasteles decorados para fiestas de cumpleaños infantiles y otras ocasiones especiales. La panadería quiere que el volumen de un pastel pequeño sea de 351 pulgadas cúbicas. El pastel tiene la forma de un sólido rectangular. Quieren que la longitud del pastel sea cuatro pulgadas más larga que el ancho del pastel y que la altura del pastel sea un tercio del ancho. ¿Cuáles deberían ser las dimensiones del molde para pasteles?
Solución:
Comienza escribiendo una ecuación para el volumen del pastel. El volumen de un sólido rectangular viene dado por (V = lwh ). Se nos dijo que la longitud debe ser cuatro pulgadas más larga que el ancho, por lo que podemos expresar la longitud del pastel como (l = w + 4 ). Se nos dio que la altura del pastel es un tercio del ancho, por lo que podemos expresar la altura del pastel como (h = dfrac {1} {3} w ). Escribamos el volumen del pastel en términos de ancho del pastel.
Sustituye el volumen dado en esta ecuación.
(351 = 13w ^ 3 + 43w ^ 2 ) Sustituye 351 por V. (1053 = w ^ 3 + 4w ^ 2 ) Multiplica ambos lados por 3. (0 = w ^ 3 + 7w ^ 2−1053 ) Resta 1053 de ambos lados.La regla de signos de Descartes nos dice que hay una solución positiva. El teorema del cero racional nos dice que los posibles ceros racionales son ( pm 1, ± 3, ± 9, ± 13, ± 27, ± 39, ± 81, ± 117, ± 351, ) y (± 1053 ) Podemos usar la división sintética para probar estos posibles ceros. Solo los números positivos tienen sentido como dimensiones para un pastel, por lo que no necesitamos probar ningún valor negativo. Comencemos probando valores que tengan más sentido como dimensiones para una torta de hoja pequeña. Use la división sintética para verificar (x = 1 ).
.jpg?revision=1)
Dado que 1 no es una solución, comprobaremos (x = 3 ).
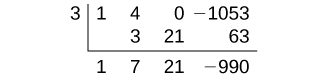
Dado que 3 tampoco es una solución, probaremos (x = 9 ).

Synthetic division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.
(l=w+4=9+4=13) and (h=dfrac{1}{3}w=dfrac{1}{3}(9)=3)The sheet cake pan should have dimensions 13 inches by 9 inches by 3 inches
![]() (PageIndex{7})
(PageIndex{7})
A shipping container in the shape of a rectangular solid must have a volume of 84 cubic meters. The client tells the manufacturer that, because of the contents, the length of the container must be one meter longer than the width, and the height must be one meter greater than twice the width. What should the dimensions of the container be?
Solution:
3 meters by 4 meters by 7 meters
Medios
Access these online resources for additional instruction and practice with zeros of polynomial functions.
Key Concepts
- To find (f(k)), determine the remainder of the polynomial (f(x)) when it is divided by (x−k). This is known as the Remainder Theorem. See Example (PageIndex{1}) .
- According to the Factor Theorem, (k) is a zero of (f(x)) if and only if ((x−k)) is a factor of (f(x)). See Example(PageIndex{2}) .
- According to the Rational Zero Theorem, each rational zero of a polynomial function with integer coefficients will be equal to a factor of the constant term divided by a factor of the leading coefficient. See Example (PageIndex{3}) and Example (PageIndex{4}) .
- When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
- Synthetic division can be used to find the zeros of a polynomial function. See Example (PageIndex{5}) .
- According to the Fundamental Theorem, every polynomial function with degree greater than 0 has at least one complex zero. See Example (PageIndex{6}) .
- Allowing for multiplicities, a polynomial function will have the same number of factors as its degree. Each factor will be in the form ((x−c)), where (c) is a complex number. See Example (PageIndex{7}) .
- The number of positive real zeros of a polynomial function is either the number of sign changes of the function or less than the number of sign changes by an even integer.
- The number of negative real zeros of a polynomial function is either the number of sign changes of (f(−x)) or less than the number of sign changes by an even integer. See Example (PageIndex{8}) .
- Polynomial equations model many real-world scenarios. Solving the equations is easiest done by synthetic division. See Example (PageIndex{9}) .
Glossary
Descartes’ Rule of Signs
a rule that determines the maximum possible numbers of positive and negative real zeros based on the number of sign changes of (f(x)) and (f(−x))
Factor Theorem
(k) is a zero of polynomial function (f(x)) if and only if ((x−k)) is a factor of (f(x))
Fundamental Theorem of Algebra
a polynomial function with degree greater than 0 has at least one complex zero
Linear Factorization Theorem
allowing for multiplicities, a polynomial function will have the same number of factors as its degree, and each factor will be in the form ((x−c)), where (c) is a complex number
Rational Zero Theorem
the possible rational zeros of a polynomial function have the form (frac{p}{q}) where (p) is a factor of the constant term and (q) is a factor of the leading coefficient.
Remainder Theorem
if a polynomial (f(x)) is divided by (x−k),then the remainder is equal to the value (f(k))
