
Esta sección está dedicada a explicar una serie de atajos importantes para multiplicar binomios. Estos son patrones extremadamente importantes que producirán los mismos productos calculados en secciones anteriores. Es esencial que los lectores practiquen hasta que se vuelvan competentes utilizando cada uno de los patrones presentados en esta sección.
El método FOIL
Considere el producto de dos binomios ((x + 3) (x + 6) ). Ya sabemos cómo encontrar el producto de estos dos binomios; multiplicamos (x ) por ambos términos de (x + 6 ), luego multiplicamos (3 ) por ambos términos de (x + 6 ).
[(x + 3) (x + 6) = x ^ {2} +6 x + 3 x + 18 nonumber ]
Normalmente combinamos términos similares, pero detenemos el proceso en este punto para introducir el patrón llamado método FOIL. Las letras en la palabra FOIL significan “Primero”, “Exterior”, “Interior” y “Último”.
Veamos cómo podemos conectar estos términos al producto ((x + 3) (x + 6) ).
- Las flechas indican los términos en las posiciones “Primero” en cada binomio. Si multiplica los términos en la posición “Primero”, obtendrá (x ^ 2 ). [{ Color {Red} underbrace { color {Black} (x + 3) (x} _ {F} } +6) nonumber ]
- Las flechas indican los términos en las posiciones “externas” en cada binomio. Si multiplica los términos en las posiciones “Exterior”, obtendrá (6x ). [{ Color {Red} underbrace { color {Black} (x + 3) (x + 6} _ {O} }) nonumber ]
- Las flechas indican los términos en las posiciones “internas” en cada binomio. Si multiplica los términos en las posiciones “internas”, obtendrá (3x ). [(X + { color {Red} underbrace { color {Black} {3) (x}} _ {I}} +6) nonumber ]
- Las flechas indican los términos en las posiciones “Últimas” en cada binomio. Si multiplica los términos en las posiciones “Últimas”, obtendrá (18 ). [(X + { color {Red} underbrace { color {Black} {3) (x + 6}} _ {L }}) nonumber ]
El siguiente diagrama muestra la conexión entre “Primero”, “Exterior”, “Interior”, “Último” y la respuesta.
[(x + 3) (x + 6) = begin {array} {ccccccc} color {Red} {F} & {} & color {Red} {O} & {} & color {Rojo} {I} y {} y color {Rojo} {L} \ x ^ {2} y + y 6x y + y 3x y + y 18 end {array} nonumber ]
Ejemplo ( PageIndex {1} )
Utilice el método FOIL para simplificar: ((x + 5) (x + 7) )
Solución
Multiplica las posiciones “Primero”: (x ^ 2 ). Multiplique las posiciones “externas”: (7x ). Multiplique las posiciones “internas”: (5x ). Multiplique las posiciones “Últimas”: (35 ).
[(x + 5) (x + 7) = begin {array} {ccccccc} color {Red} {F} & {} & color {Red} {O} & {} & color {Rojo} {I} y {} y color {Rojo} {L} \ x ^ {2} y + y 7x y + y 5x y + y 35 end {array} nonumber ]
Combinando términos similares, ((x + 5) (x + 7) = x ^ {2} +12 x + 35 )
Ejercicio ( PageIndex {1} )
Simplificar: ((x + 2) (x + 11) )
- Respuesta
-
(x ^ {2} +13 x + 22 )
Ejemplo ( PageIndex {2} )
Utilice el método FOIL para simplificar: ((2x − 7) (x − 4) )
Solución
Multiplica las posiciones “Primero”: (2x ^ 2 ). Multiplique las posiciones “externas”: (- 8x ). Multiplique las posiciones “internas”: (- 7x ). Multiplique las posiciones “Últimas”: (28 ).
[(2x-7) (x-4) = begin {array} {ccccccc} color {Red} {F} & {} & color {Red} {O} & {} & color {Rojo} {I} & {} & color {Rojo} {L} \ 2x ^ {2} & – & 8x & – & 7x & + & 28 end {array} nonumber ]
Combinando términos similares, ((2 x-7) (x-4) = 2 x ^ {2} -15 x + 28 )
Ejercicio ( PageIndex {2} )
Simplificar: ((x − 1) (4x + 5) )
- Respuesta
-
(4 x ^ {2} + x-5 )
A primera vista, el método FOIL no parece un atajo. Después de todo, si simplemente usamos la propiedad distributiva en el producto del Ejemplo ( PageIndex {2} ), obtenemos el mismo resultado rápido.
[ begin {alineado} (2 x-7) (x-4) & = 2 x (x-4) -7 (x-4) \ & = 2 x ^ {2} -8 x -7 x + 28 \ & = 2 x ^ {2} -15 x + 28 end {alineado} nonumber ]
El método FOIL se convierte en un verdadero atajo cuando agregamos los resultados “Externo” e “Interno” en nuestra cabeza.
Atajo FOIL
Para multiplicar dos binomios, siga estos pasos:
- Multiplica los términos en las posiciones “Primero”.
- Multiplique los términos en las posiciones “Exterior” e “Interior” y combine los resultados mentalmente (si son términos similares).
- Multiplica los términos en las posiciones “Últimas”.
Ejemplo ( PageIndex {3} )
Utilice el acceso directo FOIL para simplificar: ((3x + 8) (2x − 1) )
Solución
Cada uno de los siguientes pasos se realiza mentalmente.
- Multiplica los términos en las posiciones “Primero”: (6x ^ 2 )
- Multiplica los términos en las posiciones “Exterior” e “Interior” y agrega los resultados mentalmente: (- 3x + 16x = 13x )
- Multiplica los términos en las posiciones “Últimas”: (- 8 )
Escriba la respuesta sin pasos intermedios: ((3 x + 8) (2 x-1) = 6 x ^ {2} +13 x-8 )
Ejercicio ( PageIndex {3} )
Simplificar: ((2z − 3) (5z − 1) )
- Respuesta
-
(10 z ^ {2} -17 z + 3 )
Ejemplo ( PageIndex {4} )
Use el acceso directo FOIL para simplificar: ((4y − 3) (5y + 2) )
Solución
Cada uno de los siguientes pasos se realiza mentalmente.
- Multiplica los términos en las posiciones “Primero”: (20y ^ 2 )
- Multiplique los términos en las posiciones “Exterior” e “Interior” y agregue los resultados mentalmente: (8y − 15y = −7y )
- Multiplica los términos en las posiciones “Últimas”: (- 6 )
Escriba la respuesta sin pasos intermedios: ((4 y-3) (5 y + 2) = 20 y ^ {2} -7 y-6 )
Ejercicio ( PageIndex {4} )
Simplificar: ((7 x + 2) (2 x-3) )
- Respuesta
-
(14 x ^ {2} -17 x-6 )
La diferencia de cuadrados
Podemos usar el atajo FOIL para multiplicar ((a + b) (a − b) ).
- Multiplica los términos en las posiciones “Primero”: (a ^ 2 )
- Multiplique los términos en las posiciones “Exterior” e “Interior” y agregue los resultados mentalmente: (ab − ab = 0 )
- Multiplica los términos en las posiciones “Últimas”: (- b ^ 2 )
Por lo tanto, ((a + b) (a-b) = a ^ {2} -b ^ {2} ) . Observe cómo el lado derecho (a ^ 2 −b ^ 2 ) es la diferencia de dos cuadrados. Esto lleva al siguiente acceso directo.
La diferencia de cuadrados
Si tiene términos idénticos en las posiciones “Primero” y términos idénticos en las posiciones “Últimas”, pero un conjunto está separado con un signo más mientras que el otro está separado por un signo menos, entonces proceda de la siguiente manera: [19459001 ]
- Cuadrar el término “Primero”.
- Cuadrar el término “Último”.
- Coloque un signo menos entre los resultados
Es decir,
[(a + b) (a-b) = a ^ {2} -b ^ {2} nonumber ]
Nota
Si no tiene términos idénticos en las posiciones “Primero” y “Último”, con un conjunto separado con un signo más y el otro con un signo menos, entonces no tiene la diferencia de cuadrados patrón y debe encontrar alguna otra forma de multiplicar. Por ejemplo, ((x + 3) (x − 3) ) es un ejemplo de la diferencia del patrón de cuadrados, pero ((2y + 3) (2y − 5) ) no lo es.
Ejemplo ( PageIndex {5} )
Use el método abreviado de diferencia de cuadrados para simplificar: ((x + 3) (x− 3) )
Solución
Observe cómo los términos en la posición “Primera” son idénticos, al igual que los términos en la posición “Última”, con un conjunto separado por un signo más y el otro con un signo menos. Por lo tanto, esta es la diferencia del patrón de cuadrados y procedemos de la siguiente manera:
- Al cuadrado el término en la posición “Primera”: (x ^ 2 )
- Al cuadrado el término en la posición “Última”: ((- 3) ^ 2 = 9 )
- Separe los cuadrados con un signo menos.
Es decir:
[ begin {alineado} (x + 3) (x-3) & = x ^ {2} – (3) ^ {2} \ & = x ^ {2} -9 end {alineado } nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en ((x + 3) (x − 3) = x ^ 2 −9 ).
Ejercicio ( PageIndex {5} )
Simplifica: ((x + 5) (x − 5) )
- Respuesta
-
(x ^ {2} -25 )
Ejemplo ( PageIndex {6} )
Use el método abreviado de diferencia de cuadrados para simplificar: ((8y + 7z) (8y − 7z) )
Solución
Observe cómo los términos en la posición “Primera” son idénticos, al igual que los términos en la posición “Última”, con un conjunto separado por un signo más y el otro con un signo menos. Por lo tanto, esta es la diferencia del patrón de cuadrados y procedemos de la siguiente manera:
- Al cuadrado el término en la posición “Primera”: ((8y) ^ 2 = 64 y ^ 2 )
- Al cuadrado el término en la posición “Última”: ((7z) ^ 2 = 49 z ^ 2 )
- Separe los cuadrados con un signo menos.
Es decir:
[ begin {alineado} (8 y + 7 z) (8 y-7 z) & = (8 y) ^ {2} – (7 z) ^ {2} \ & = 64 y ^ {2} -49 z ^ {2} end {alineado} nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en ((8 y + 7 z) (8 y-7 z) = 64 y ^ { 2} -49 z ^ {2} )
Ejercicio ( PageIndex {6} )
Simplifique: ((3a − 6b) (3a + 6b) )
- Respuesta
-
(9 a ^ {2} -36 b ^ {2} )
Ejemplo ( PageIndex {7} )
Use el método abreviado de diferencia de cuadrados para simplificar: ( left (x ^ {3} -5 y ^ {2} right) left (x ^ {3} +5 y ^ {2} right) )
Solución
Observe cómo los términos en la posición “Primera” son idénticos, al igual que los términos en la posición “Última”, con un conjunto separado por un signo más y el otro con un signo menos. Por lo tanto, esta es la diferencia del patrón de cuadrados y procedemos de la siguiente manera:
- Al cuadrado el término en la posición “Primera”: ((x ^ 3) ^ 2 = x ^ 6 )
- Al cuadrado el término en la posición “Última”: ((5y ^ 2) ^ 2 = 25 y ^ 4 )
- Separe los cuadrados con un signo menos.
Es decir:
[ begin {alineado} left (x ^ {3} -5 y ^ {2} right) left (x ^ {3} +5 y ^ {2} right) & = left (x ^ {3} right) ^ {2} – left (5 y ^ {2} right) ^ {2} \ & = x ^ {6} -25 y ^ {4} end {alineado } nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en ( left (x ^ {3} -5 y ^ {2} right) left (x ^ {3} +5 y ^ {2} right) = x ^ {6} -25 y ^ {4} )
Ejercicio ( PageIndex {7} )
Simplifique: ( left (2 y ^ {4} + z ^ {3} right) left (2 y ^ {4} -z ^ {3} right) )
- Respuesta
-
(4 años ^ {8} -z ^ {6} )
Cuadrando un binomio
Antes de demostrar el procedimiento correcto para cuadrar un binomio, compartiremos primero uno de los errores más comunes cometidos en álgebra.
¡Advertencia! ¡Esto es incorrecto!
Uno de los errores más comunes cometidos en álgebra es la suposición de que:
[(a + b) ^ {2} = a ^ {2} + b ^ {2} nonumber ]
El hecho de que esto sea incorrecto se verifica fácilmente. Sustituya (3 ) por (a ) y (4 ) por (b ).
[ begin {alineado} (3 + 4) ^ {2} & = 3 ^ {2} + 4 ^ {2} \ 7 ^ {2} & = 3 ^ {2} + 4 ^ {2} \ 49 & = 9 + 16 end {alineado} nonumber ]
¡Claramente esto es incorrecto!
Entonces, ¿cuál es la respuesta correcta? Primero, ((a + b) ^ {2} = (a + b) (a + b) ) . Ahora podemos usar el atajo FOIL.
- Multiplica los términos en las posiciones “Primero”: (a ^ 2 )
- Multiplica los términos en las posiciones “Exterior” e “Interior” y agrega los resultados mentalmente: (ab + ab = 2ab )
- Multiplica los términos en las posiciones “Últimas”: (b ^ 2 )
Por lo tanto, la respuesta correcta es ((a + b) ^ {2} = a ^ {2} +2 a b + b ^ {2} ) . Esto nos lleva al siguiente atajo para cuadrar un binomio.
Cuadrando un binomio
Para cuadrar un binomio, como ((a + b) ^ 2 ), realice los siguientes pasos:
- Al cuadrado el término “Primero”: (a ^ 2 )
- Multiplica los términos “Primero” y “Último” y duplica el resultado: (2ab )
- Al cuadrado el término “Último”: (b ^ 2 )
Es decir:
[(a + b) ^ {2} = a ^ {2} +2 a b + b ^ {2} nonumber ]
Ejemplo ( PageIndex {8} )
Utilice el cuadrado un acceso directo binomial para expandir: ((x + 5) ^ {2} )
Solución
Siga estos pasos:
- Al cuadrado el primer término: (x ^ 2 )
- Multiplique los términos “Primero” y “Último” y duplique el resultado: (2 (x) (5) = 10x )
- Al cuadrado el término “Último”: (5 ^ 2 = 25 )
Así:
[ begin {alineado} (x + 5) ^ {2} & = x ^ {2} +2 (x) (5) + (5) ^ {2} \ & = x ^ {2 } +10 x + 25 end {alineado} nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en ((x + 5) ^ {2} = x ^ {2} +10 x + 25 )
Ejercicio ( PageIndex {8} )
Simplificar: ((x + 3) ^ {2} )
- Respuesta
-
(x ^ {2} +6 x + 9 )
Comentario
Los estudiantes a menudo se niegan a aprender el atajo de “cuadrar un binomio”, y señalan que pueden usar la técnica FOIL con la misma facilidad o una simple aplicación de la propiedad distributiva para llegar al mismo resultado. Desafortunadamente, si no aprende el atajo “cuadrar un binomio” perjudicará severamente a los estudiantes, ya que este patrón es un componente importante de muchos procedimientos en futuros cursos de matemáticas.
Ejemplo ( PageIndex {9} )
Usa el cuadrado un acceso directo binomial para expandir: ((3 x + 7 y) ^ {2} )
Solución
Siga estos pasos:
- Al cuadrado el primer término: ((3x) ^ 2 = 9x ^ 2 )
- Multiplique los términos “Primero” y “Último” y duplique el resultado: (2 (3x) (7y) = 42xy )
- Al cuadrado el término “Último”: ((7y) ^ 2 = 49 y ^ 2 )
Así:
[ begin {alineado} (3 x + 7 y) ^ {2} & = (3 x) ^ {2} +2 (3 x) (7 y) + (7 y) ^ {2} \ & = 9 x ^ {2} +42 x y + 49 y ^ {2} end {alineado} nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en ((3 x + 7 y) ^ {2} = 9 x ^ {2} + 42 x y + 49 y ^ {2} )
Ejercicio ( PageIndex {9} )
Simplifique: ((2 y + 3 z) ^ {2} )
- Respuesta
-
(4 y ^ {2} +12 y z + 9 z ^ {2} )
En el siguiente ejemplo, cuando cuadramos un binomio con un signo menos, nos encargamos del signo menos “sumando lo contrario”.
Ejemplo ( PageIndex {10} )
Usa el cuadrado de un acceso directo binomial para expandir: ( left (4 a ^ {2} -5 b ^ {3} right) ^ {2} )
Solución
Agregue lo contrario: ((4a ^ 2−5b ^ 3) ^ 2 = (4 a ^ 2 + (- 5b ^ 3)) ^ 2 ). Ahora siga estos pasos:
- Al cuadrado el primer término: ((4a ^ 2) ^ 2 = 16 a ^ 4 )
- Multiplique los términos “Primero” y “Último” y duplique el resultado: (2 (4a ^ 2) (- 5b ^ 3) = −40a ^ 2b ^ 3 )
- Al cuadrado el término “Último”: ((- 5b ^ 3) ^ 2 = 25 b ^ 6 )
Así:
[ begin {alineado} left (4 a ^ {2} -5 b ^ {3} right) ^ {2} & = left (4 a ^ {2} + left (-5 b ^ {3} right) right) ^ {2} \ & = left (4 a ^ {2} right) ^ {2} +2 left (4 a ^ {2} right) left (-5 b ^ {3} right) + left (-5 b ^ {3} right) ^ {2} \ & = 16 a ^ {4} -40 a ^ {2} b ^ { 3} +25 b ^ {6} end {alineado} nonumber ]
Nota
Debe practicar este patrón hasta que pueda pasar directamente del enunciado del problema a la respuesta sin escribir ningún trabajo intermedio, como en [ left (4 a ^ {2} -5 b ^ {3} right) ^ {2} = 16 a ^ {4} -40 a ^ {2} b ^ {3} +25 b ^ {6} nonumber ]
Ejercicio ( PageIndex {10} )
Simplifique: ( left (3 x ^ {4} -5 z ^ {2} right) ^ {2} )
- Respuesta
-
(9 x ^ {8} -30 x ^ {4} z ^ {2} +25 z ^ {4} )
Ejemplo ( PageIndex {10} ) nos muestra que si estamos cuadrando una diferencia, el término medio será menos. Es decir, la única diferencia entre ((a + b) ^ 2 ) y ((a − b) ^ 2 ) es el signo del término medio.
Cuadrando un binomio
Los atajos para cuadrar un binomio son:
[(a + b) ^ {2} = a ^ {2} +2 a b + b ^ {2} nonumber ]
[(a-b) ^ {2} = a ^ {2} -2 a b + b ^ {2} nonumber ]
Ejemplo ( PageIndex {11} )
Utilice el cuadrado un acceso directo binomial para expandir: ( left (x ^ {3} -y ^ {3} right) ^ {2} )
Solución
Use el patrón ((a − b) ^ 2 = a ^ 2 −2ab + b ^ 2 ). Cuadre el término “Primero”, multiplique los términos “Primero” y “Último” y duplique el resultado, luego cuadre el término “Último”. Debido al signo menos, el término medio será menos, pero todos los demás términos son más.
[ begin {alineado} left (x ^ {3} -y ^ {3} right) ^ {2} & = left (x ^ {3} right) ^ {2} -2 left (x ^ {3} right) left (y ^ {3} right) + left (y ^ {3} right) ^ {2} \ & = x ^ {6} -2 x ^ {3} y ^ {3} + y ^ {6} end {alineado} nonumber ]
Ejercicio ( PageIndex {11} )
Simplifique: ( left (a ^ {2} -3 b ^ {5} right) ^ {2} )
- Respuesta
-
(a ^ {4} -6 a ^ {2} b ^ {5} +9 b ^ {10} )
Una solicitud
En el ejemplo ( PageIndex {7} ), encontramos el área del cuadrado exterior sumando las áreas de sus partes (ver Figura ( PageIndex {1} )). Recuerde que la respuesta fue (A = x ^ 2 + 6x + 9 ).
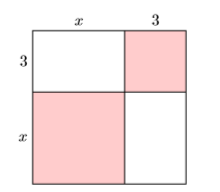
Ahora que tenemos la cuadratura de un atajo binomial, podemos simplificar el proceso de encontrar el área del cuadrado exterior cuadrando su lado. Es decir:
[A = (x + 3) ^ {2} nonumber ]
Ahora podemos usar el cuadrado de la técnica binomial para expandir.
[ begin {array} {l} {= x ^ {2} +2 (x) (3) + (3) ^ {2}} \ {= x ^ {2} +6 x + 9} end {array} nonumber ]
Tenga en cuenta que esto es lo mismo que la respuesta encontrada al sumar las cuatro partes del cuadrado en el Ejemplo ( PageIndex {7} ).
