
En esta sección nos concentramos en encontrar sumas y diferencias de expresiones racionales. Sin embargo, antes de comenzar, necesitamos revisar algunas ideas y técnicas fundamentales.
Primero y principal es el concepto del múltiplo de un entero. Esto se explica mejor con un ejemplo simple. Los múltiplos de 8 son el conjunto de enteros ( {8 k: k text {es un entero} } ). En otras palabras, si multiplica 8 por (0, pm 1, pm 2, pm 3, pm 4 ), etc., produce lo que se conoce como los múltiplos de 8.
[ text {Los múltiplos de} 8 text {son:} 0, pm 8, pm 16, pm 24, pm 32, text {etc.} ]
Sin embargo, para nuestros propósitos, solo los múltiplos positivos son de interés. Entonces diremos:
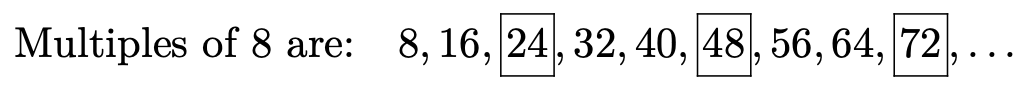
Del mismo modo, podemos enumerar los múltiplos positivos de 6.
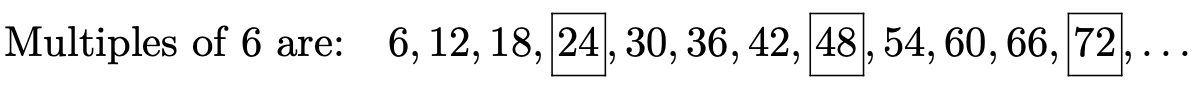
Hemos enmarcado los números que son múltiplos de 8 y 6. Estos se llaman los múltiplos comunes de 8 y 6.
[ text {múltiplos comunes de} 8 text {y} 6 text {son:} 24,48,72, ldots ]
El más pequeño de esta lista de múltiplos comunes de 8 y 6 se llama el mínimo común múltiplo de 8 y 6. Usaremos la siguiente notación para representar el mínimo común múltiplo de 8 y 6: MCM (8, 6).
Con suerte, ahora te sentirás cómodo con la siguiente definición.
Definición: Mínimo común múltiplo (MCM)
Sea (a ) y (b ) ser enteros. El mínimo común múltiplo de ayb, denotado LCM (a, b), es el múltiplo positivo más pequeño que ayb tienen en común.
Para números más grandes, enumerar múltiplos hasta encontrar uno en común puede ser poco práctico y llevar mucho tiempo. Busquemos el mínimo común múltiplo de 8 y 6 por segunda vez, solo que esta vez usemos una técnica diferente.
Primero, escribe cada número como un producto de primos en forma exponencial.
[ begin {array} {l} {8 = 2 ^ {3}} \ {6 = 2 cdot 3} end {array} ]
Aquí está la regla.
Un procedimiento para encontrar el MCM
Para encontrar el MCM de dos enteros, proceda de la siguiente manera.
- Expresa la factorización prima de cada número entero en formato exponencial.
- Para encontrar el mínimo común múltiplo, escriba cada número primo que aparezca, luego fije el máximo exponente de ese primo que aparece.
En nuestro ejemplo, los números primos que ocurren son 2 y 3. La potencia más alta de 2 que ocurre es (2 ^ {3} ). La potencia más alta de 3 que ocurre es (3 ^ {1} ). Por lo tanto, el MCM (8, 6) es
[ operatorname {LCM} (8,6) = 2 ^ {3} cdot 3 ^ {1} = 24 ]
Tenga en cuenta que este resultado es idéntico al resultado anterior al enumerar todos los múltiplos comunes y elegir el más pequeño.
Probemos con un ejemplo más difícil.
Ejemplo ( PageIndex {1} )
Encuentra el mínimo común múltiplo de 24 y 36.
Solución
Usando la primera técnica, enumeramos los múltiplos de cada número, enmarcando los múltiplos en común.
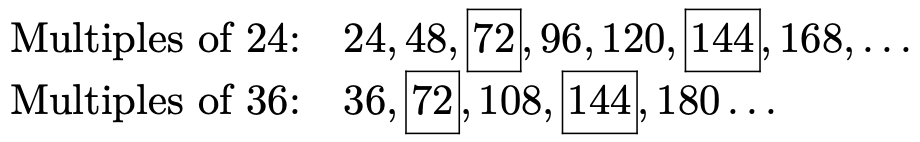
Los múltiplos en común son 72, 144, etc., y el mínimo común múltiplo es MCM (24, 36) = 72.
Ahora, usemos nuestra segunda técnica para encontrar el mínimo común múltiplo (LCM). Primero, exprese cada número como un producto de primos en formato exponencial.
[ begin {array} {l} {24 = 2 ^ {3} cdot 3} \ {36 = 2 ^ {2} cdot 3 ^ {2}} end {array} ]
Para encontrar el mínimo común múltiplo, escriba cada primo que ocurra y fije la potencia más alta de ese primo que ocurra. Por lo tanto, la potencia más alta de 2 que ocurre es (2 ^ {3} ), y la potencia más alta de 3 que ocurre es (3 ^ {2} ). Por lo tanto, el mínimo común múltiplo es [ operatorname {LCM} (24,36) = 2 ^ {3} cdot 3 ^ {2} = 8 cdot 9 = 72 ]
Suma y resta definidas
Imagina una pizza que se ha cortado en 12 rebanadas iguales. Luego, cada porción de pizza representa 1/12 de la pizza completa.
Si Jimmy come 3 rebanadas, entonces ha consumido 3/12 de toda la pizza. Si Margaret come 2 rebanadas, entonces ha consumido 2/12 de toda la pizza. Está claro que juntos han consumido [ frac {3} {12} + frac {2} {12} = frac {5} {12} ]
de la pizza. ¡Parecería que agregar dos fracciones con un denominador común es tan simple como comer pizza! Con suerte, la siguiente definición parecerá razonable.
Definición
Para sumar dos fracciones con un denominador común , como a / cy b / c, suma los numeradores y divide por el denominador común. En símbolos,
[ frac {a} {c} + frac {b} {c} = frac {a + b} {c} ]
Observe cómo esta definición concuerda precisamente con nuestro consumo de pizza discutido anteriormente. Aquí hay algunos ejemplos de sumar fracciones que tienen denominadores comunes.
[ begin {array} {llllll} { frac {5} {21} + frac {3} {21}} & {=} & { frac {5 + 3} {21}} & { frac {2} {x + 2} + frac {x-3} {x + 2}} & {=} & { frac {2+ (x-3)} {x + 2}} \ {} & {=} & { frac {8} {21}} & {} & {=} & { frac {2 + x-3} {x + 2}} \ {} &&& {} & { =} & { frac {x-1} {x + 2}} end {array} ]
La resta funciona de la misma manera que la suma.
Definición
Para restar dos fracciones con un denominador común, como a / cy b / c, reste los numeradores y divida por el común denominador. En símbolos,
[ frac {a} {c} – frac {b} {c} = frac {a-b} {c} ]
Aquí hay algunos ejemplos de restar fracciones que ya tienen denominadores comunes.
[ begin {array} {llllll} { frac {5} {21} – frac {3} {21}} & {=} & { frac {5-3} {21}} & { frac {2} {x + 2} – frac {x-3} {x + 2}} & {=} & { frac {2- (x-3)} {x + 2}} \ {} & {=} & { frac {2} {21}} & {} & {=} & { frac {2-x + 3} {x + 2}} \ {} &&& {} & { =} & { frac {5-x} {x + 2}} end {array} ]
En el ejemplo de la derecha, tenga en cuenta que es extremadamente importante utilizar símbolos de agrupación al restar numeradores. Tenga en cuenta que el signo menos delante de la expresión entre paréntesis cambia el signo de cada término dentro de los paréntesis.
Hay momentos en que un cambio de signo proporcionará un denominador común.
Ejemplo ( PageIndex {2} )
Simplifique [ frac {x} {x-3} – frac {2} {3-x} ] Indique todas las restricciones.
Solución
A primera vista, parece que no tenemos un denominador común. A segunda vista, si hacemos un cambio de signo en la segunda fracción, podría ayudar. Entonces, en la segunda fracción, neguemos el denominador y la barra de fracción para obtener [ frac {x} {x-3} – frac {2} {3-x} = frac {x} {x-3} + frac {2} {x-3} = frac {x + 2} {x-3} ]
Los denominadores x − 3 o 3 − x son cero cuando x = 3. Por lo tanto, 3 es un valor restringido. Para todos los demás valores de x, el lado izquierdo de
[ frac {x} {x-3} – frac {2} {3-x} = frac {x + 2} {x-3} ]
es idéntico al lado derecho.
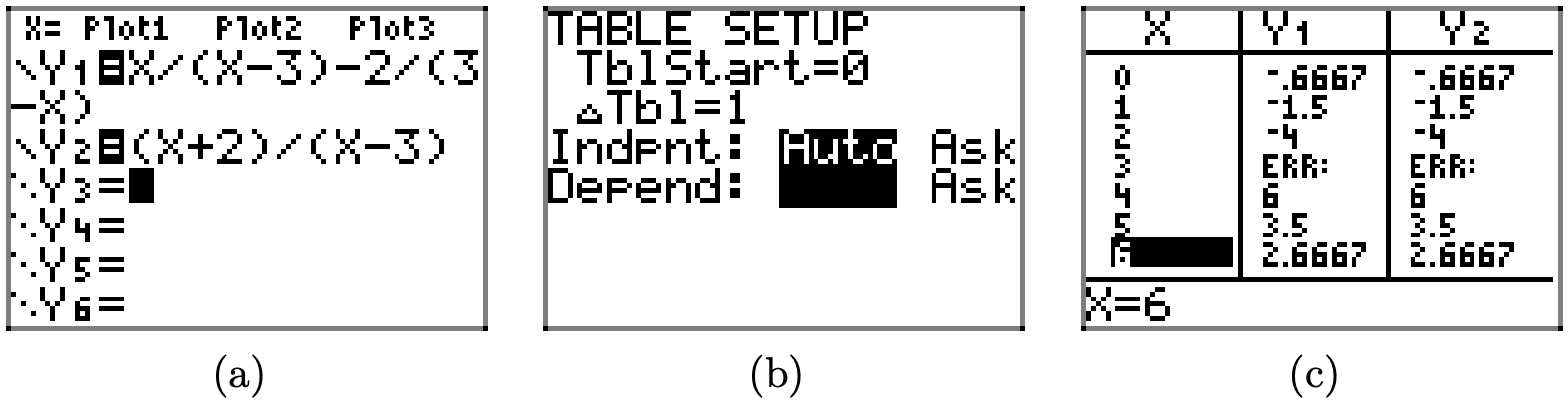
Esto se prueba fácilmente usando la utilidad de tabla en la calculadora gráfica, como se muestra en la secuencia de capturas de pantalla en la Figura ( PageIndex {1} ). Primero cargue los lados izquierdo y derecho de la ecuación (7) en Y1 e Y2 en el menú Y = de su calculadora gráfica, como se muestra en la Figura ( PageIndex {1} ) (a). Presione 2nd TBLSET y realice los cambios que se muestran en la Figura ( PageIndex {1} ) (b). Presione 2nd TABLE para producir la tabla que se muestra en la Figura ( PageIndex {1} ) (c). Tenga en cuenta el mensaje ERR (error) en la restricción x = 3, pero tenga en cuenta también el acuerdo de Y1 e Y2 para todos los demás valores de x.
Fracciones equivalentes
Si corta una pizza en cuatro partes iguales, luego consume dos de las cuatro rebanadas, ha consumido la mitad de la pizza. Esto motiva el hecho de que [ frac {1} {2} = frac {2} {4} ]. De hecho, si corta la pizza en seis partes iguales, luego consume tres rebanadas, ha consumido la mitad de la pizza, por lo que es justo decir que 3/6 = 1/2. De hecho, todas las siguientes fracciones son equivalentes:
[ frac {1} {2} = frac {2} {4} = frac {3} {6} = frac {4} {8} = frac {5} {10} = frac {6} {12} = frac {7} {14} = cdots ]
Una forma más formal de demostrar que 1/2 y 7/14 son iguales es comenzar con el hecho de que 1/2 = 1/2 × 1, luego reemplazar 1 con 7/7 y multiplicar.
[ frac {1} {2} = frac {1} {2} times color {blue} {1} = frac {1} {2} times color {blue} { frac {7} {7}} = frac {7} {14} ]
Aquí hay otro ejemplo de este principio en acción, solo que esta vez reemplazamos 1 con (x – 2) / (x – 2).
[ frac {3} {x + 2} = frac {3} {x + 2} cdot color {blue} {1} = frac {3} {x + 2} cdot color {azul} { frac {x-2} {x-2}} = frac {3 (x-2)} {(x + 2) (x-2)} ]
En el siguiente ejemplo reemplazamos 1 con (x (x – 3)) / (x (x – 3)).
[ frac {2} {x-4} = frac {2} {x-4} cdot color {blue} {1} = frac {2} {x-4} cdot color {azul} { frac {x (x-3)} {x (x-3)}} = frac {2 x (x-3)} {x (x-4) (x-3)} ]
Ahora, apliquemos el concepto de fracciones equivalentes para sumar y restar fracciones con diferentes denominadores.
Sumar y restar fracciones con diferentes denominadores
En esta sección mostramos a nuestros lectores cómo sumar y restar fracciones con diferentes denominadores. Por ejemplo, supongamos que se nos pide agregar las siguientes fracciones.
[ frac {5} {12} + frac {5} {18} ]
Primero, debemos encontrar un “denominador común”. Afortunadamente, la maquinaria para encontrar el “denominador común” ya está en su lugar. Resulta que el mínimo común denominador de 12 y 18 es el mínimo común múltiplo de 12 y 18.
[ begin {alineado} 18 & = 2 cdot 3 ^ {2} \ 12 & = 2 ^ {2} cdot 3 \ operatorname {LCD} (12,18) & = 2 ^ {2} cdot 3 ^ {2} = 36 end {alineado} ]
El siguiente paso es crear fracciones equivalentes utilizando la pantalla LCD como denominador. Entonces, en el caso del 5/12,
[ frac {5} {12} = frac {5} {12} cdot color {blue} {1} = frac {5} {12} cdot color {blue} { frac {3} {3}} = frac {15} {36} ]
En el caso del 5/18, [ frac {5} {18} = frac {5} {18} cdot color {blue} {1} = frac {5} {18} cdot color {blue} { frac {2} {2}} = frac {10} {36} ]
Si reemplazamos las fracciones en la ecuación (8) con sus fracciones equivalentes, entonces podemos sumar los numeradores y dividirlos por el denominador común, como en
[ frac {5} {12} + frac {5} {18} = frac {15} {36} + frac {10} {36} = frac {15 + 10} {36 } = frac {25} {36} ]
Examinemos un método para organizar el trabajo que sea más compacto. Considere la siguiente disposición, donde hemos usado el color para resaltar la forma de 1 requerida para convertir las fracciones a fracciones equivalentes con un denominador común de 36.
[ begin {alineado} frac {5} {12} + frac {5} {18} & = frac {5} {12} cdot color {azul} { frac {3} {3}} + frac {5} {18} cdot color {azul} { frac {2} {2}} \ & = frac {15} {36} + frac {10} {36 } \ & = frac {25} {36} end {alineado} ]
Veamos un ejemplo más complicado.
Ejemplo ( PageIndex {3} )
Simplifique la expresión [ frac {x + 3} {x + 2} – frac {x + 2} {x + 3} ] Indique todas las restricciones.
Solución
Los denominadores ya están factorizados. Si tomamos cada factor que aparece con la potencia exponencial más alta que aparece, nuestro mínimo común denominador es (x + 2) (x + 3). Nuestra primera tarea es hacer fracciones equivalentes que tengan este denominador común.
[ begin {alineado} frac {x + 3} {x + 2} – frac {x + 2} {x + 3} & = frac {x + 3} {x + 2} cdot color {azul} { frac {x + 3} {x + 3}} – frac {x + 2} {x + 3} cdot color {azul} { frac {x + 2} {x +2}} \ & = frac {x ^ {2} +6 x + 9} {(x + 2) (x + 3)} – frac {x ^ {2} +4 x + 4} { (x + 2) (x + 3)} end {alineado} ]
Ahora, resta los numeradores y divide por el común denominador.
[ begin {alineado} frac {x + 3} {x + 2} – frac {x + 2} {x + 3} & = frac { left (x ^ {2} +6 x + 9 right) – left (x ^ {2} +4 x + 4 right)} {(x + 2) (x + 3)} \ & = frac {x ^ {2} +6 x + 9-x ^ {2} -4 x-4} {(x + 2) (x + 3)} \ & = frac {2 x + 5} {(x + 2) (x + 3) } end {alineado} ]
Tenga en cuenta el uso de paréntesis cuando restamos los numeradores. Observe además cómo el signo menos niega cada término en la expresión entre paréntesis que sigue al signo menos.
Consejo
Siempre use símbolos de agrupación al restar los numeradores de fracciones.
En la respuesta final, los factores x + 2 y x + 3 en el denominador son cero cuando x = −2 o x = −3. Estas son las restricciones. Ningún otro denominador, en el problema original o en el cuerpo de nuestro trabajo, proporciona restricciones adicionales.
Por lo tanto, para todos los valores de x, excepto los valores restringidos −2 y −3, el lado izquierdo de
[ frac {x + 3} {x + 2} – frac {x + 2} {x + 3} = frac {2 x + 5} {(x + 2) (x + 3) } ]
es idéntico al lado derecho. Esta afirmación se prueba fácilmente en la calculadora gráfica que se evidencia en la secuencia de capturas de pantalla en la Figura ( PageIndex {2} ). Observe el mensaje ERR (error) en cada valor restringido de x en la Figura ( PageIndex {2} ) (c), pero también tenga en cuenta el acuerdo de Y1 e Y2 para todos los demás valores de x.
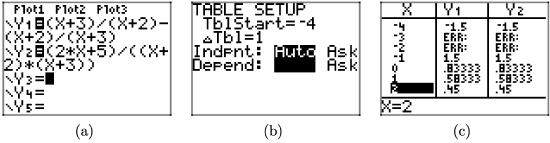
Veamos otro ejemplo.
Ejemplo ( PageIndex {4} )
Simplifique la expresión [ frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} ]. Indique todas las restricciones.
Solución
Primero, factoriza cada denominador. [ frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} = frac {4} {(x + 1) ( x + 5)} – frac {2} {(x + 3) (x + 5)} ]
El mínimo común denominador, o mínimo común múltiplo (MCM), requiere que anotemos cada factor que ocurre, luego fijemos la potencia más alta de ese factor que ocurre. Debido a que todos los factores en los denominadores se elevan a una potencia comprendida de uno, el LCD (mínimo común denominador) o LCM es (x + 1) (x + 5) (x + 3).
Luego, hacemos fracciones equivalentes con este denominador común.
[ begin {alineado} frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} & = frac { 4} {(x + 1) (x + 5)} cdot color {azul} { frac {x + 3} {x + 3}} – frac {2} {(x + 3) (x + 5)} cdot color {azul} { frac {x + 1} {x + 1}} \ & = frac {4 x + 12} {(x + 3) (x + 5) (x + 1)} – frac {2 x + 2} {(x + 3) (x + 5) (x + 1)} end {alineado} ]
Resta los numeradores y divide por el común denominador. Asegúrese de usar símbolos de agrupación, particularmente con el signo menos que está en juego.
[ begin {alineado} frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} & = frac { (4 x + 12) – (2 x + 2)} {(x + 3) (x + 5) (x + 1)} \ & = frac {4 x + 12-2 x-2} {( x + 3) (x + 5) (x + 1)} \ & = frac {2 x + 10} {(x + 3) (x + 5) (x + 1)} end {alineado} ]
Finalmente, siempre debemos asegurarnos de que nuestra respuesta se reduzca a los términos más bajos. Con ese pensamiento en mente, factorizamos el numerador con la esperanza de que podamos obtener un factor común para cancelar.
[ begin {alineado} frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} & = frac { 2 (x + 5) } {(x + 3) (x + 5) (x + 1)} \ & = frac {2 (x + 5)} {(x + 3) (x + 5) (x + 1)} \ & = frac {2} {(x + 3) (x + 1)} end {alineado} ]
Los denominadores tienen factores de x + 3, x + 5 y x + 1, por lo que las restricciones son x = −3, x = −5 y x = −1, respectivamente. Para todos los demás valores de x, el lado izquierdo de
[ frac {4} {x ^ {2} +6 x + 5} – frac {2} {x ^ {2} +8 x + 15} = frac {2} {(x + 3) (x + 1)} ]
es idéntico a su lado derecho. Nuevamente, esto se prueba fácilmente usando la función de tabla de la calculadora gráfica, como se muestra en las capturas de pantalla en la Figura ( PageIndex {3} ). Nuevamente, tenga en cuenta los mensajes ERR (error) en cada valor restringido de x, pero también tenga en cuenta que Y1 e Y2 están de acuerdo con todos los demás valores de x.
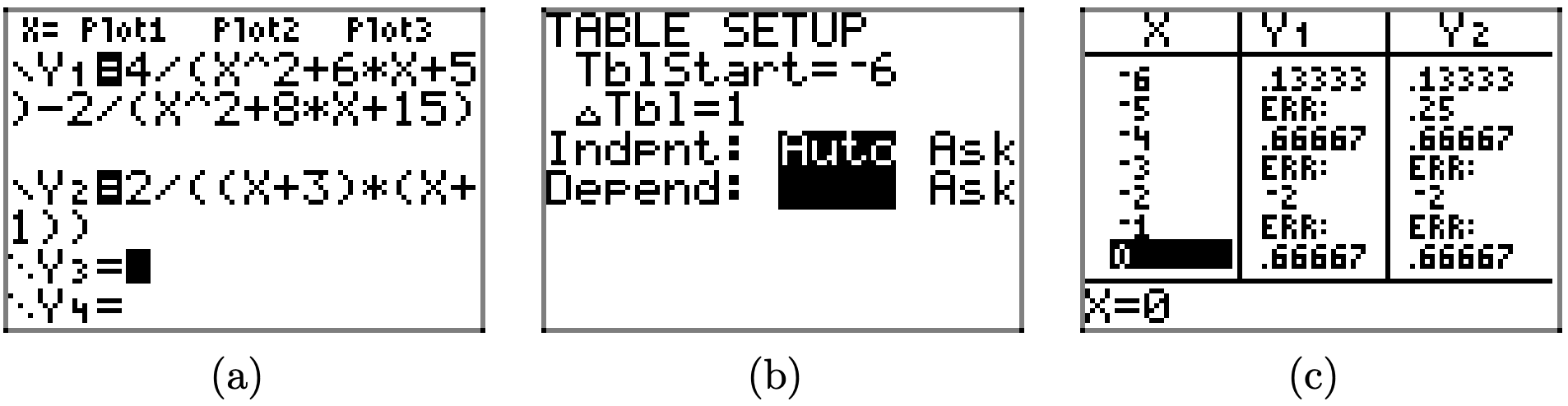
Veamos otro ejemplo.
Ejemplo ( PageIndex {5} )
Simplifique la expresión [ frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} ]. Indique todas las restricciones.
Solución
Primero, factorizar todos los denominadores.
[ frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} = frac {x-3 } {(x + 1) (x-1)} + frac {1} {x + 1} – frac {1} {1-x} ]
Si no tenemos cuidado, podríamos sentir la tentación de tomar uno de cada factor y usar (x + 1) (x− 1) (1 − x) como denominador común. Sin embargo, primero hagamos dos negaciones de la última de las tres fracciones a la derecha, negando la barra de fracción y el denominador para obtener
[ frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} = frac {x-3 } {(x + 1) (x-1)} + frac {1} {x + 1} + frac {1} {x-1} ]
Ahora podemos ver que un denominador común de (x + 1) (x – 1) será suficiente. Hagamos fracciones equivalentes con este denominador común.
[ begin {alineado} frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} & = frac {x-3} {(x + 1) (x-1)} + frac {1} {x + 1} cdot color {blue} { frac {x-1} {x-1} } + frac {1} {x-1} cdot color {azul} { frac {x + 1} {x + 1}} \ & = frac {x-3} {(x + 1) (x-1)} + frac {x-1} {(x + 1) (x-1)} + frac {x + 1} {(x + 1) (x-1)} end {alineado } ]
Suma los numeradores y divide por el común denominador. Aunque los símbolos de agrupación no son tan críticos en este problema (debido a los signos más), todavía consideramos que es una buena práctica usarlos.
[ begin {alineado} frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} & = frac {(x-3) + (x-1) + (x + 1)} {(x + 1) (x-1)} \ & = frac {3 x-3} {(x + 1 ) (x-1)} end {alineado} ]
Finalmente, asegúrese siempre de que su respuesta final se reduzca a los términos más bajos. Con ese pensamiento en mente, factorizamos el numerador con la esperanza de que podamos obtener un factor común para cancelar.
[ begin {alineado} frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} & = frac {3 (x-1)} {(x + 1) (x-1)} \ & = frac {3 (x-1) } {(x + 1) [19459036 ] (x-1) } \ & = frac {3} {x + 1} end {alineado} ]
Los factores x + 1 yx – 1 en el denominador producen restricciones x = −1 yx = 1, respectivamente. Sin embargo, para todos los demás valores de x, el lado izquierdo de
[ frac {x-3} {x ^ {2} -1} + frac {1} {x + 1} – frac {1} {1-x} = frac {3} { x + 1} ]
es idéntico al lado derecho. Nuevamente, esto se verifica fácilmente en la calculadora gráfica como se muestra en la secuencia de capturas de pantalla en la Figura ( PageIndex {4} ).
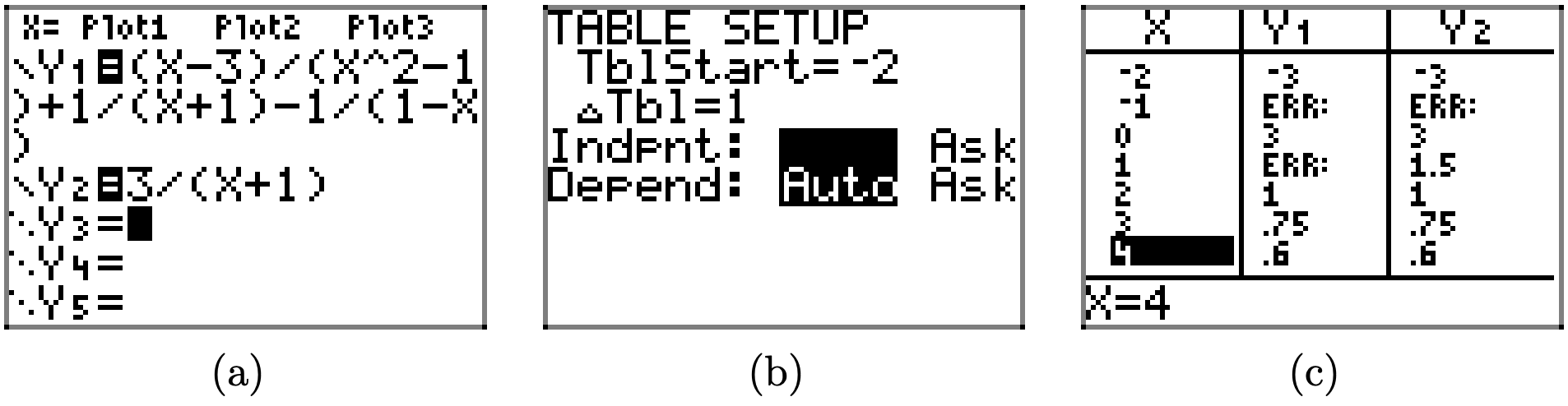
Nuevamente, tenga en cuenta los mensajes ERR (error) en cada restricción, pero también tenga en cuenta que los valores de Y1 e Y2 coinciden con todos los demás valores de x.
Veamos un ejemplo usando la notación de función.
Ejemplo ( PageIndex {6} )
Si la función fyg están definidas por las reglas [f (x) = frac {x} {x + 2} quad text {y} quad g (x) = frac {1} {x} ], simplifica f (x) – g (x).
Solución
Primero, [f (x) -g (x) = frac {x} {x + 2} – frac {1} {x} ]
Tenga en cuenta lo tentador que sería cancelar. Sin embargo, cancelar sería un error en esta situación, porque la resta requiere un denominador común.
[ begin {alineado} f (x) -g (x) & = frac {x} {x + 2} cdot color {blue} { frac {x} {x}} – frac {1} {x} cdot color {azul} { frac {x + 2} {x + 2}} \ & = frac {x ^ {2}} {x (x + 2)} – frac {x + 2} {x (x + 2)} end {alineado} ]
Resta los numeradores y divide por el común denominador. Esto requiere que “distribuyamos” el signo menos.
[ begin {alineado} f (x) -g (x) & = frac {x ^ {2} – (x + 2)} {x (x + 2)} \ & = frac {x ^ {2} -x-2} {x (x + 2)} end {alineado} ]
Este resultado es válido para todos los valores de x excepto 0 y −2. Dejamos que nuestros lectores verifiquen que este resultado se reduzca a los términos más bajos. Es posible que también desee verificar el resultado en su calculadora.
Ejercicio
En Ejercicios 1 – 16 , suma o resta las expresiones racionales, como se indica, y simplifica tu respuesta. Indique todas las restricciones.
EJERCICIO ( PageIndex {1} )
( frac {7x ^ 2−49x} {x − 6} + frac {42} {x − 6} )
- Respuesta
-
7 (x − 1), proporcionado (x ne 6 ).
EJERCICIO ( PageIndex {2} )
( frac {2x ^ 2−110} {x − 7} – frac {12} {7 − x} )
EJERCICIO ( PageIndex {3} )
( frac {27x− 9x ^ 2} {x + 3} + frac {162} {x + 3} )
- Respuesta
-
−9 (x − 6), proporcionado (x ne −3 ).
EJERCICIO ( PageIndex {4} )
( frac {2x ^ 2−28} {x + 2} – frac {10x} {x + 2} )
EJERCICIO ( PageIndex {5} )
( frac {4x ^ 2−8} {x − 4} + frac {56} {4 − x} )
- Respuesta
-
4 (x + 4), proporcionado (x ne 4 ).
EJERCICIO ( PageIndex {6} )
( frac {4x ^ 2} {x − 2} – frac {36x − 56} {x − 2} )
EJERCICIO ( PageIndex {7} )
( frac {9x ^ 2} {x − 1} + frac {72x − 63} {1 − x} )
- Respuesta
-
9 (x − 7), proporcionado (x ne 1 ).
EJERCICIO ( PageIndex {8} )
( frac {5x ^ 2 + 30} {x − 6} – frac {35x} {x − 6} )
EJERCICIO ( PageIndex {9} )
( frac {4x ^ 2−60x} {x − 7} + frac {224} {x − 7} )
- Respuesta
-
4 (x − 8), proporcionado (x ne 7 ).
EJERCICIO ( PageIndex {10} )
( frac {3x ^ 2} {x − 7} – frac {63−30x} {7 − x} )
EJERCICIO ( PageIndex {11} )
( frac {3x ^ 2} {x − 2} – frac {48−30x} {2 − x} )
- Respuesta
-
3 (x − 8), proporcionado (x ne 2 ).
EJERCICIO ( PageIndex {12} )
( frac {4x ^ 2−164} {x − 6} – frac {20} {6 − x} )
EJERCICIO ( PageIndex {13} )
( frac {9x ^ 2} {x − 2} – frac {81x − 126} {x − 2} )
- Respuesta
-
9 (x − 7), proporcionado (x ne 2 ).
EJERCICIO ( PageIndex {14} )
( frac {9x ^ 2} {x − 8} + frac {144x − 576} {8 − x} )
EJERCICIO ( PageIndex {15} )
( frac {3x ^ 2−12} {x − 3} + frac {15} {3 − x} )
- Respuesta
-
3 (x + 3), proporcionado (x ne 3 ).
EJERCICIO ( PageIndex {16} )
( frac {7x ^ 2} {x − 9} – frac {112x − 441} {x − 9} )
En Ejercicios 17 – 34 , suma o resta las expresiones racionales, como se indica, y simplifica tu respuesta. Indique todas las restricciones.
EJERCICIO ( PageIndex {17} )
( frac {3x} {x ^ 2−6x + 5} + frac {15} {x ^ 2−14x + 45} )
- Respuesta
-
Proporcionado (x ne 5, 1, 9 ),
( frac {3 (x + 1)} {(x − 1) (x − 9)} )
EJERCICIO ( PageIndex {18} )
( frac {7x} {x ^ 2−4x} + frac {28} {x ^ 2−12x + 32} )
EJERCICIO ( PageIndex {19} )
( frac {9x} {x ^ 2 + 4x − 12} – frac {54} {x ^ 2 + 20x + 84} )
- Respuesta
-
Proporcionado (x ne −6, 2, −14 ),
( frac {9 (x + 2)} {(x − 2) (x + 14)} )
EJERCICIO ( PageIndex {20} )
( frac {9x} {x ^ 2−25} – frac {45} {x ^ 2 + 20x + 75} )
EJERCICIO ( PageIndex {21} )
( frac {5x} {x ^ 2−21x + 98} – frac {35} {7x − x ^ 2} )
- Respuesta
-
Proporcionado (x ne 7, 14, 0 ),
( frac {5 (x + 14)} {x (x − 14)} )
EJERCICIO ( PageIndex {22} )
( frac {7x} {7x − x ^ 2} + frac {147} {x ^ 2 + 7x − 98} )
EJERCICIO ( PageIndex {23} )
( frac {−7x} {x ^ 2−8x + 15} – frac {35} {x ^ 2−12x + 35} )
- Respuesta
-
Proporcionado (x ne 5, 3, 7 ),
( frac {−7 (x + 3)} {(x − 3) (x − 7)} )
EJERCICIO ( PageIndex {24} )
( frac {−6x} {x ^ 2 + 2x} + frac {12} {x ^ 2 + 6x + 8} )
EJERCICIO ( PageIndex {25} )
( frac {−9x} {x ^ 2−12x + 32} – frac {36} {x ^ 2−4x} )
- Respuesta
-
Proporcionado (x ne 4, 8, 0 ),
( frac {−9 (x + 8)} {x (x − 8)} )
EJERCICIO ( PageIndex {26} )
( frac {5x} {x ^ 2−12x + 32} – frac {20} {4x − x ^ 2} )
EJERCICIO ( PageIndex {27} )
( frac {6x} {x ^ 2−21x + 98} – frac {42} {7x − x ^ 2} )
- Respuesta
-
Proporcionado (x ne 7, 14, 0 ),
( frac {6 (x + 14)} {x (x − 14)} )
EJERCICIO ( PageIndex {28} )
( frac {−2x} {x ^ 2−3x − 10} + frac {4} {x ^ 2 + 11x + 18} )
EJERCICIO ( PageIndex {29} )
( frac {−9x} {x ^ 2−6x + 8} – frac {18} {x ^ 2−2x} )
- Respuesta
-
Proporcionado (x ne 2,4,0 ),
( frac {−9 (x + 4)} {x (x − 4)} )
EJERCICIO ( PageIndex {30} )
( frac {6x} {5x − x ^ 2} + frac {90} {x ^ 2 + 5x − 50} )
EJERCICIO ( PageIndex {31} )
( frac {8x} {5x − x ^ 2} + frac {120} {x ^ 2 + 5x − 50} )
- Respuesta
-
Proporcionado (x ne 5, 0, −10 ),
( frac {−8} {x + 10} )
EJERCICIO ( PageIndex {32} )
( frac {−5x} {x ^ 2 + 5x} + frac {25} {x ^ 2 + 15x + 50} )
EJERCICIO ( PageIndex {33} )
( frac {−5x} {x ^ 2 + x − 30} + frac {30} {x ^ 2 + 23x + 102} )
- Respuesta
-
Proporcionado (x ne −6, 5, −17 ),
( frac {−5 (x + 5)} {(x − 5) (x + 17)} )
EJERCICIO ( PageIndex {34} )
( frac {9x} {x ^ 2 + 12x + 32} – frac {36} {x ^ 2 + 4x} )
EJERCICIO ( PageIndex {35} )
Deje
(f (x) = frac {8x} {x ^ 2 + 6x + 8} )
y
(g (x) = frac {16} {x ^ 2 + 2x} )
Calcule f (x) −g (x) y simplifique su respuesta.
- Respuesta
-
Proporcionado (x ne −2, −4, 0 ),
( frac {8 (x − 4)} {x (x + 4)} )
EJERCICIO ( PageIndex {36} )
Deje
(f (x) = frac {−7x} {x ^ 2 + 8x + 12} )
y
(g (x) = frac {42} {x ^ 2 + 16x + 60} )
Calcule f (x) + g (x) y simplifique su respuesta.
EJERCICIO ( PageIndex {37} )
Deje
(f (x) = frac {11x} {x ^ 2 + 12x + 32} )
y
(g (x) = frac {44} {- 4x − x ^ 2} )
Calcule f (x) + g (x) y simplifique su respuesta.
- Respuesta
-
Proporcionado (x ne −4, −8, 0 ),
( frac {11 (x − 8)} {x (x + 8)} )
EJERCICIO ( PageIndex {38} )
Deje
(f (x) = frac {8x} {x ^ 2−6x} )
y
(g (x) = frac {48} {x ^ 2−18x + 72} )
Calcule f (x) + g (x) y simplifique su respuesta.
EJERCICIO ( PageIndex {39} )
Deje
(f (x) = frac {4x} {- x − x ^ 2} )
y
(g (x) = frac {4} {x ^ 2 + 3x + 2} )
Calcule f (x) + g (x) y simplifique su respuesta.
- Respuesta
-
Proporcionado (x ne −1, 0, −2 ),
( frac {−4} {x + 2} )
EJERCICIO ( PageIndex {40} )
Deje
(f (x) = frac {5x} {x ^ 2 − x − 12} )
y
(g (x) = frac {15} {x ^ 2 + 13x + 30} )
Calcule f (x) −g (x) y simplifique su respuesta.
