
Hemos visto en secciones anteriores que un monomio es el producto de un número y uno o más factores variables, cada uno elevado a una potencia integral positiva, como en (- 3 x ^ {2} ) o 4 (x ^ {3} y ^ {4} ). También hemos visto que un binomio es la suma o diferencia de dos términos monomiales, como en (3 x + 5, x ^ {2} +4, ) o (3 xy ^ {2} = 2 x ^ {2} y ). También hemos visto que un trinomio es la suma o diferencia de tres términos monomiales, como en (x ^ {2} -2 x-3 ) o (x ^ {2} -4 x y + 5 y ^ {2} ).
La palabra raíz “poli” significa “muchos”, como en polígono (muchos lados) o políglota (que habla muchos idiomas, multilingüe). En álgebra, la palabra polinomio significa “muchos términos”, donde la frase “muchos términos” puede interpretarse en el sentido de un número arbitrario, pero finito, de términos. En consecuencia, un monomio podría considerarse un polinomio, al igual que binomios y trinomios. En nuestro trabajo, nos concentraremos en su mayor parte en polinomios de una sola variable. Lo que sigue es una definición más formal de un polinomio en una sola variable (x ).
Definición: polinomios
La función p, definida por
[p (x) = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + cdots + a_ {n} x ^ {n} label {1} ]
se denomina polinomio en (x ).
Hay varios puntos importantes que hacer sobre esta definición.
Nota
- El polinomio en nuestra definición en la ecuación ref {1} está organizado en potencias ascendentes de (x ). Podríamos organizar fácilmente nuestro polinomio en poderes descendentes de (x ), como en [p (x) = a_ {n} x ^ {n} + cdots + a_ {2} x ^ {2} + a_ {1} x + a_ {0} ]
- Los números (a_ {0}, a_ {1}, a_ {2}, dots, a_ {n} ) se denominan coeficientes del polinomio p. – Si todos los coeficientes son enteros, entonces decimos que ” (p ) es un polinomio con coeficientes enteros”. – Si todos los coeficientes son números racionales, entonces decimos que ” (p ) es un polinomio con coeficientes racionales”. – Si todos los coeficientes son números reales, entonces decimos que ” (p ) es un polinomio con coeficientes reales”.
- El grado del polinomio (p ) es (n ), la potencia más alta de (x ).
- El término principal del polinomio (p ) es el término con la mayor potencia de (x ). En el caso de la ecuación ref {2}, el término principal es un (x ^ n ).
Veamos un ejemplo.
Ejemplo ( PageIndex {1} )
Considere el polinomio
[p (x) = 3-4 x ^ {2} +5 x ^ {3} -6 x nonumber ]
Encuentre el grado, el término principal, y haga una declaración sobre los coeficientes de p.
Solución
Primero, ordena los términos polinómicos. Si usa poderes ascendentes o descendentes de x no hay diferencia. Escoge una o la otra. En potencias descendentes de x,
[p (x) = 5 x ^ {3} -4 x ^ {2} -6 x + 3 label {5} ]
pero en potencias ascendentes de (x ),
[p (x) = 3-6 x-4 x ^ {2} +5 x ^ {3} label {6} ]
En cualquier caso, Ecuación ref {5} o Ecuación ref {6}, el grado del polinomio es 3. Además, en cualquier caso, el término principal del polinomio es 5 (x ^ {3} ). Como todos los coeficientes de este polinomio son enteros, decimos que “p es un polinomio con coeficientes enteros”. Sin embargo, todos los coeficientes también son números racionales, por lo que podríamos decir que p es un polinomio con coeficientes racionales. Por lo demás, todos los coeficientes de p son números reales, por lo que también podríamos decir que p es un polinomio con coeficientes reales.
Veamos otro ejemplo.
Ejemplo ( PageIndex {2} )
Considere el polinomio
[p (x) = 3- frac {4} {3} x + frac {2} {5} x ^ {2} -9 x ^ {3} +12 x ^ {4}. ]
Encuentre el grado, el término principal y haga una declaración sobre los coeficientes de (p ).
Solución
Afortunadamente, el polinomio p ya está dispuesto en potencias ascendentes de x. El grado de p es 4 y el término principal es 12 (x ^ {4} ). No todos los coeficientes son enteros, por lo que no podemos decir que “p es un polinomio con coeficientes enteros”. Sin embargo, todos los coeficientes son números racionales, por lo que podemos decir que “p es un polinomio con coeficientes racionales”. Como todos los coeficientes de p son números reales, también podríamos decir que ” (p ) es un polinomio con coeficientes reales”.
Ejemplo ( PageIndex {3} )
Considere el polinomio [p (x) = 3- frac {4} {3} x + sqrt {2} x ^ {2} -9 x ^ {3} + pi x ^ {5} ] Encuentre el grado, el término principal y haga una declaración sobre los coeficientes de p.
Solución
Afortunadamente, el polinomio p ya está dispuesto en potencias ascendentes de x. El grado de p es 5 y el término principal es ( pi x ^ {5} ). No todos los coeficientes son enteros, por lo que no podemos decir que “p es un polinomio con coeficientes enteros”. No todos los coeficientes son números racionales, por lo que no podemos decir que “p es un polinomio con coeficientes racionales”. Sin embargo, debido a que todos los coeficientes de p son números reales, podemos decir que “p es un polinomio con coeficientes reales”.
El gráfico de (y = x ^ {n} )
El objetivo principal de esta sección es discutir el comportamiento final de polinomios arbitrarios. Por “comportamiento final”, nos referimos al comportamiento del polinomio para valores muy pequeños de x (como −1 000, −10 000, −100 000, etc.) o valores muy grandes de x (como 1 000, 10 000 , 100 000, etc.). Antes de que podamos explorar el comportamiento final de polinomios arbitrarios, primero debemos examinar el comportamiento final de algunos monomios muy básicos. Específicamente, necesitamos investigar el comportamiento final de los gráficos de (y = x ^ {n} ), donde n = 1, 2, 3,. . ..
Examinemos primero la gráfica de (y = x ^ {n} ), cuando n es par. Los gráficos son lo suficientemente simples como para dibujar, ya sea creando una tabla de puntos o usando su calculadora gráfica. En la Figura ( PageIndex {1} ) (a), (b) y (c), hemos dibujado los gráficos de (y = x ^ {2}, y = x ^ {4}, ) y (y = x ^ {6} ), respectivamente.
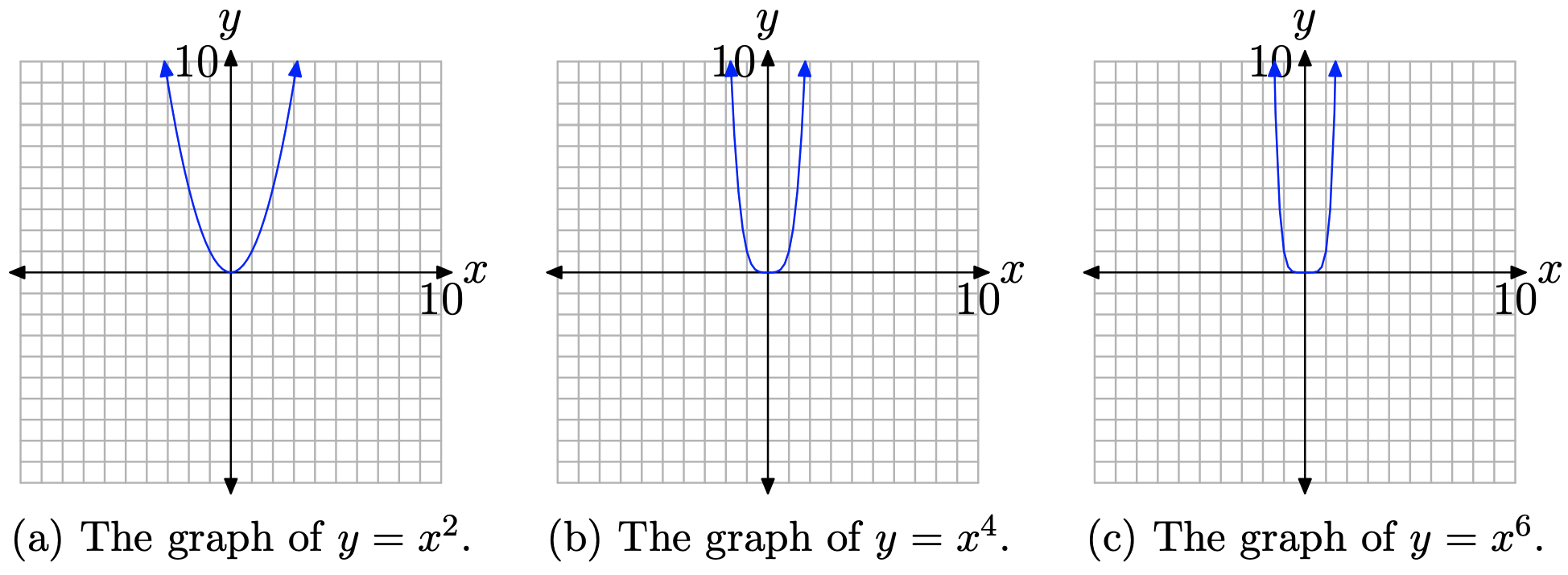
Los gráficos en la Figura ( PageIndex {1} ) comparten un rasgo importante. A medida que desliza los ojos de izquierda a derecha, cada gráfico cae desde el infinito positivo, se mueve a través del origen y luego vuelve al infinito positivo.
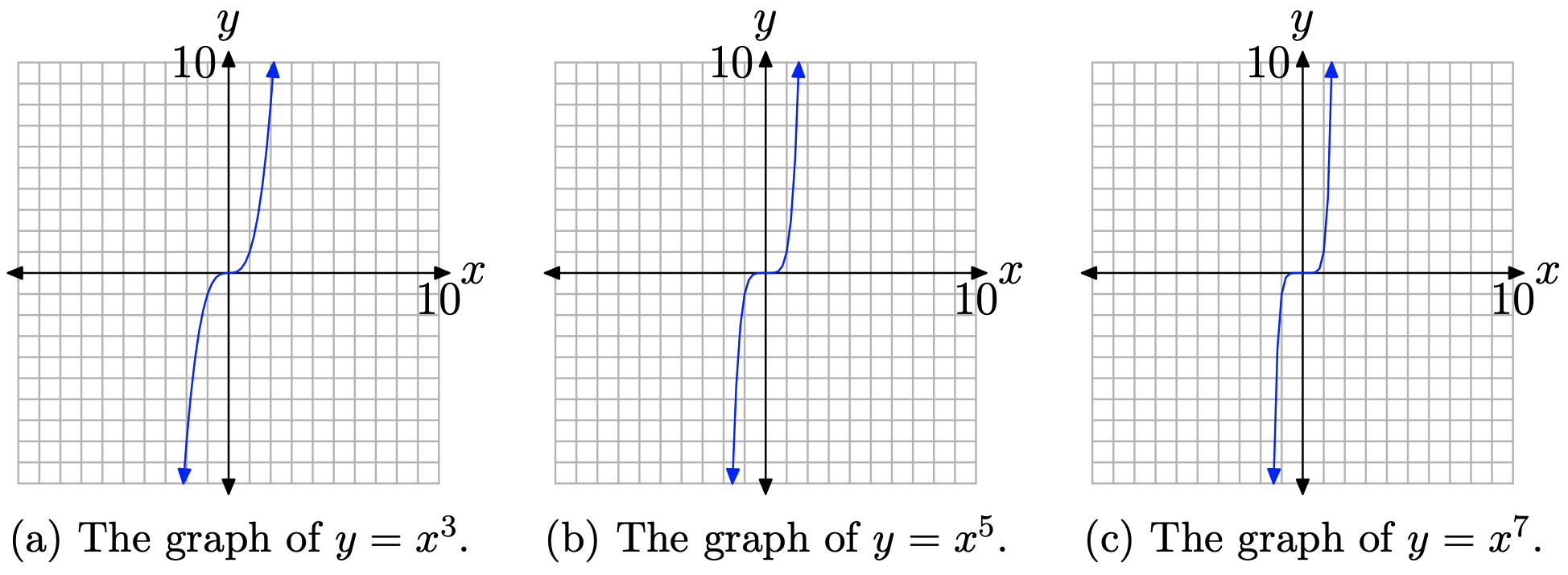
A continuación, examinemos la gráfica de (y = x ^ {n} ), cuando n es impar. Una vez más, una tabla de puntos o una calculadora gráfica ayudará a producir los gráficos de (y = x ^ {3}, y = x ^ {5}, ) y (y = x ^ {7} ), como se muestra en la Figura ( PageIndex {2} ) (a), (b) y (c), respectivamente.
Los gráficos en la Figura ( PageIndex {2} ) comparten un rasgo importante. A medida que mueve los ojos de izquierda a derecha, cada gráfico se eleva desde el infinito negativo, se mueve hacia el origen y luego se eleva hasta el infinito positivo.
El comportamiento que se muestra en la Figura ( PageIndex {1} ) y en la Figura ( PageIndex {2} ) es típico.
Propiedad 9
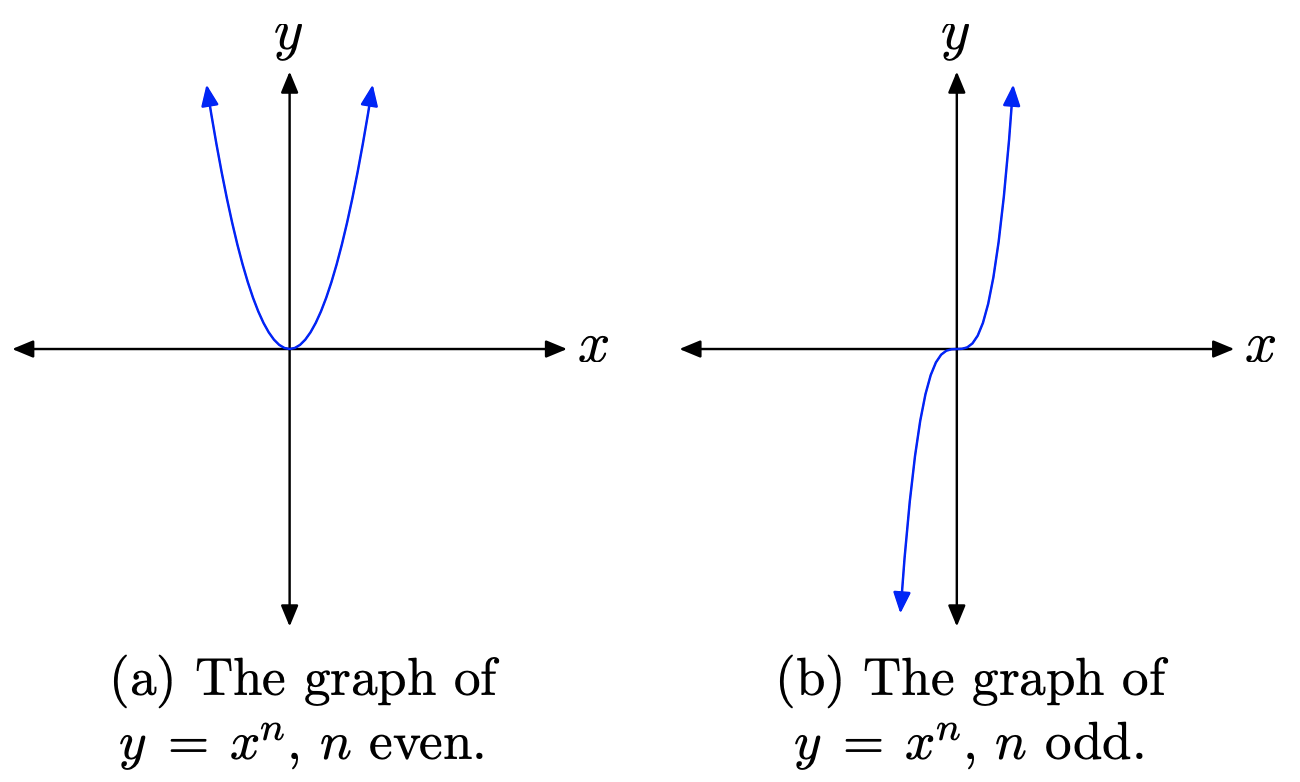
Cuando n es un número natural par, la gráfica de (y = x ^ {n} ) se verá como se muestra en la Figura ( PageIndex {3} ) (a). Si n es un número natural impar, entonces la gráfica de (y = x ^ {n} ) será similar a la que se muestra en la Figura ( PageIndex {3} ) (b).
- Cuando n es par, mientras deslizas tus ojos de izquierda a derecha, la gráfica de (y = x ^ {n} ) cae desde el infinito positivo, se mueve hacia el origen y luego vuelve al infinito positivo.
- Si n es impar, al pasar los ojos de izquierda a derecha, la gráfica de (y = x ^ {n} ) se eleva desde el infinito negativo, se mueve hacia el origen y luego se eleva hasta el infinito positivo.
La gráfica de (y = a x ^ {n} )
Ahora que conocemos la forma general de la gráfica de (y = x ^ {n} ), escalemos esta función multiplicando por una constante, como en (y = a x ^ {n} ).
En nuestro estudio de la parábola, aprendimos que si multiplicamos por un factor de a, donde a> 1, estiraremos la gráfica en la dirección vertical por un factor de a. Por el contrario, si multiplicamos la gráfica por un factor de a, donde 0
Veamos algunos ejemplos.
Ejemplo ( PageIndex {4} )
Dibuja la gráfica de (y = -2 x ^ {3} ).
Solución
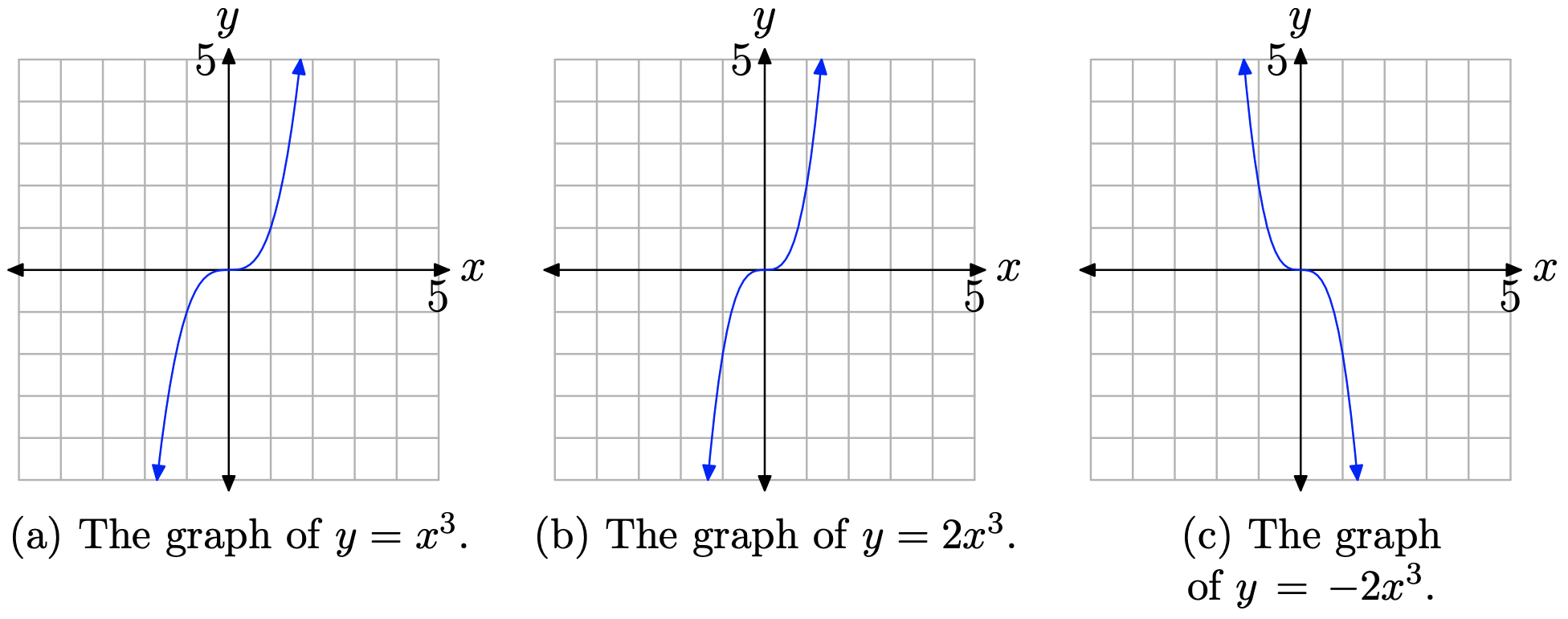
Sabemos cómo se ve la gráfica de (y = x ^ {3} ). A medida que barremos nuestros ojos de izquierda a derecha, el gráfico se eleva desde el infinito negativo, se mueve a través del origen y luego se eleva hasta el infinito positivo. Este comportamiento se muestra en la Figura ( PageIndex {4} ) (a).
Si multiplicamos por un factor de 2, entonces estiramos el gráfico original por un factor de 2 en la dirección vertical. La gráfica de (y = 2 x ^ {3} ) se muestra en la Figura ( PageIndex {4} ) (b). Tenga en cuenta el estiramiento en la dirección vertical.
Finalmente, si negamos multiplicando por −2, esto estirará la gráfica por un factor de 2, como en la Figura ( PageIndex {4} ) (b), pero también reflejará la gráfica a través de eje x La gráfica de (y = -2 x ^ {3} ) se muestra en la Figura ( PageIndex {4} ) (c).
Veamos otro ejemplo.
Ejemplo ( PageIndex {5} )
Dibuja la gráfica de (y = – frac {1} {2} x ^ {4} )
Solución
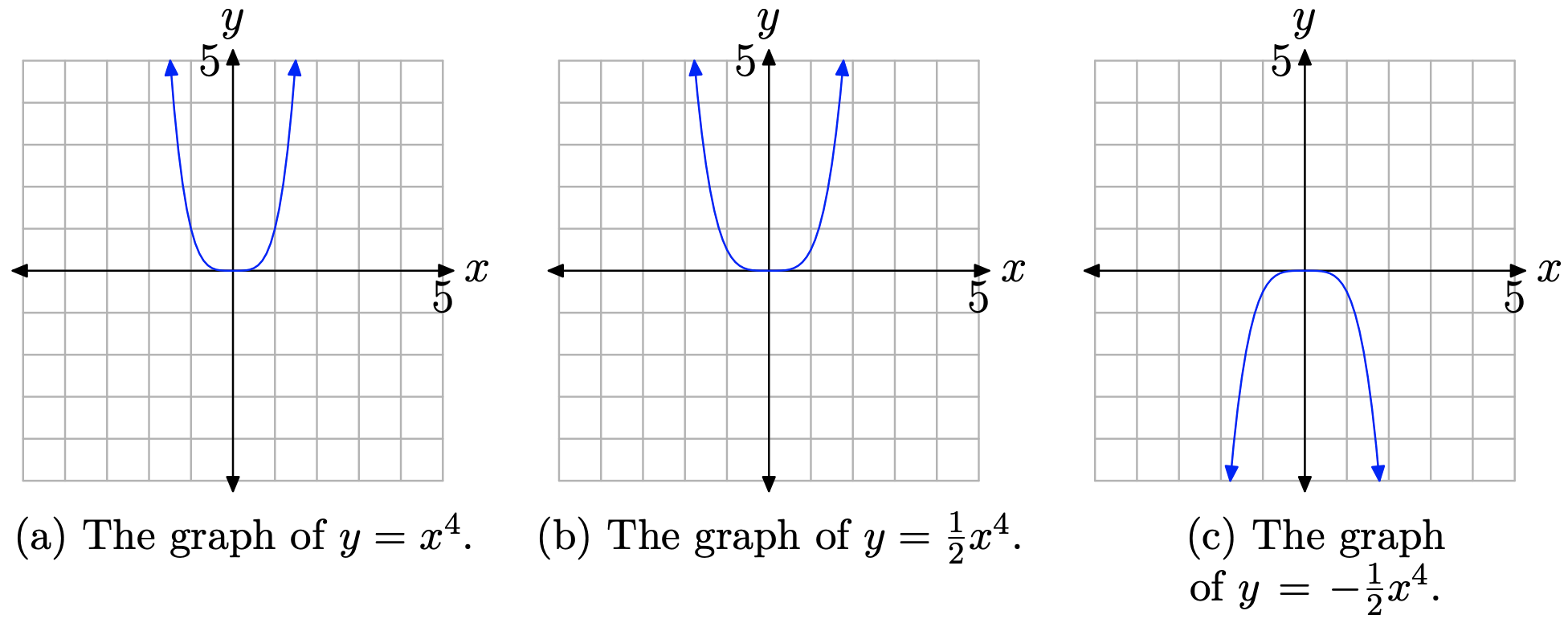
Sabemos cómo se ve la gráfica de (y = x ^ {4} ). A medida que barremos nuestros ojos de izquierda a derecha, el gráfico cae desde el infinito positivo, se mueve a través del origen y luego vuelve al infinito positivo. Este comportamiento se muestra en la Figura ( PageIndex {5} ) (a).
Si multiplicamos por 1/2, comprimiremos la gráfica por un factor de 2. Tenga en cuenta que la gráfica de (y = frac {1} {2} x ^ {4} ) en la Figura ( PageIndex {5} ) (b) está comprimido por un factor de 2 en la dirección vertical.
Finalmente, si multiplicamos por −1/2, no solo comprimiremos el gráfico por un factor de 2, sino que también reflejaremos el gráfico a través del eje x. La gráfica de (y = – frac {1} {2} x ^ {4} ) se muestra en la Figura ( PageIndex {5} ) (c).
Afortunadamente, en este punto ahora puede dibujar la gráfica de (y = a x ^ {n} ) para cualquier número real ay cualquier número natural n, par o impar, sin el uso de una calculadora. Pongamos este nuevo conocimiento para usar en la investigación del comportamiento final de los polinomios.
Fin del comportamiento
Considere el polinomio [p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ] Aquí hay un hecho clave que usaremos para determinar el comportamiento final de cualquier polinomio.
Propiedad 13
El comportamiento final de un polinomio está completamente determinado por su término principal. Es decir, el comportamiento final de la gráfica del polinomio coincidirá con el comportamiento final de la gráfica de su término principal.
En un momento, mostraremos por qué esta propiedad es verdadera. Mientras tanto, aceptemos la veracidad de esta afirmación y aplíquela al polinomio definido por la ecuación (12). El término principal del polinomio (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) es (x ^ {3} ). Conocemos el comportamiento final de la gráfica de (y = x ^ {3} ). A medida que pasemos los ojos de izquierda a derecha, la gráfica de (y = x ^ {3} ) se elevará desde el infinito negativo, se moverá a través del origen y luego continuará hasta el infinito positivo. Nos mostramos este comportamiento anteriormente en la Figura ( PageIndex {4} ) (a).
La propiedad 13 nos dice que la gráfica del polinomio (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) exhibirá el mismo comportamiento final que la gráfica de su término principal, (y = x ^ {3} ). Podemos predecir que, al barrer nuestros ojos de izquierda a derecha, la gráfica del polinomio (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) se elevará desde negativo infinito, mueve un poco, luego sube al infinito positivo. No sabemos qué sucede en el medio, pero sí sabemos qué sucede en los extremos izquierdo y derecho.
Nuestra conjetura se verifica dibujando el gráfico (use una calculadora gráfica). La gráfica del polinomio (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) se muestra en la Figura ( PageIndex {6} ). Efectivamente, cuando barremos nuestros ojos de izquierda a derecha, el gráfico en la Figura ( PageIndex {6} ) se eleva desde el infinito negativo como se predijo, se mueve un poco, luego continúa su ascenso al infinito positivo.
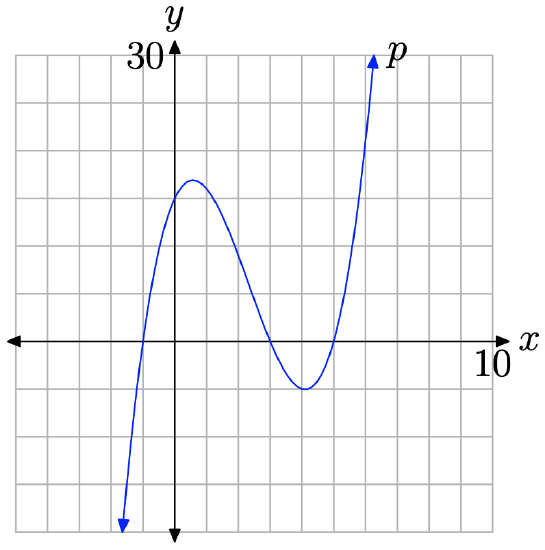
¿Por qué funciona? ¿Por qué la Propiedad 13 predice con tanta precisión el comportamiento final de este polinomio?
[p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ]
Podemos demostrar por qué factorizando primero el término principal.
[p (x) = x ^ {3} left (1- frac {7} {x} + frac {7} {x ^ {2}} + frac {15} {x ^ {3}} right) ]
Ahora, haga la siguiente pregunta. ¿Qué le sucede al polinomio a medida que avanzamos hacia el extremo derecho? Es decir, ¿qué le sucede al polinomio cuando usamos valores grandes de x, como 1 000, 10 000 o incluso 100 000?
Considere la fracción 7 / x. Como el numerador se fija en 7 y el denominador se hace cada vez más grande (crece sin límite), la fracción se acerca cada vez más a cero. Los estudiantes de cálculo usarían la notación
[ lim _ {x rightarrow infty} frac {7} {x} = 0 ]
No se desanime por la notación. Estamos usando una notación matemática sofisticada para una idea muy simple que dice “A medida que x se aproxima al infinito, la fracción 7 / x se acerca a cero”
Usando un razonamiento similar, cada una de las fracciones en la ecuación (14) va a cero a medida que x va al infinito (aumenta sin límite). Por lo tanto, a medida que x se hace más y más grande (a medida que avanzamos más y más hacia la derecha),
[ lim _ {x rightarrow infty} p (x) = lim _ {x rightarrow infty} x ^ {3} left (1- frac {7} {x} + frac {7} {x ^ {2}} + frac {15} {x ^ {3}} right) aprox x ^ {3} (1-0 + 0 + 0 + 0) aprox x ^ { 3} ]
Es decir, a medida que x aumenta sin límite, la gráfica de (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) debe aproximarse a la gráfica de (y = x ^ {3} ).
Usando un razonamiento similar, cada una de las fracciones en la ecuación (14) va a cero como x va a menos infinito. Es decir, si está poniendo números para x como −1 000, −10 000, −100 000 y similares, las fracciones en la ecuación (14) irán a cero. Por lo tanto, el polinomio p (x) aún debe acercarse a su término principal x 3 para valores muy pequeños de x (a medida que x se acerca a (- infty )).
Si superpone la gráfica de (y = x ^ {3} ) en la gráfica de (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) , como en la Figura ( PageIndex {7} ), está claro que el polinomio p tiene el mismo comportamiento final que el gráfico de su término principal (y = x ^ {3} ).
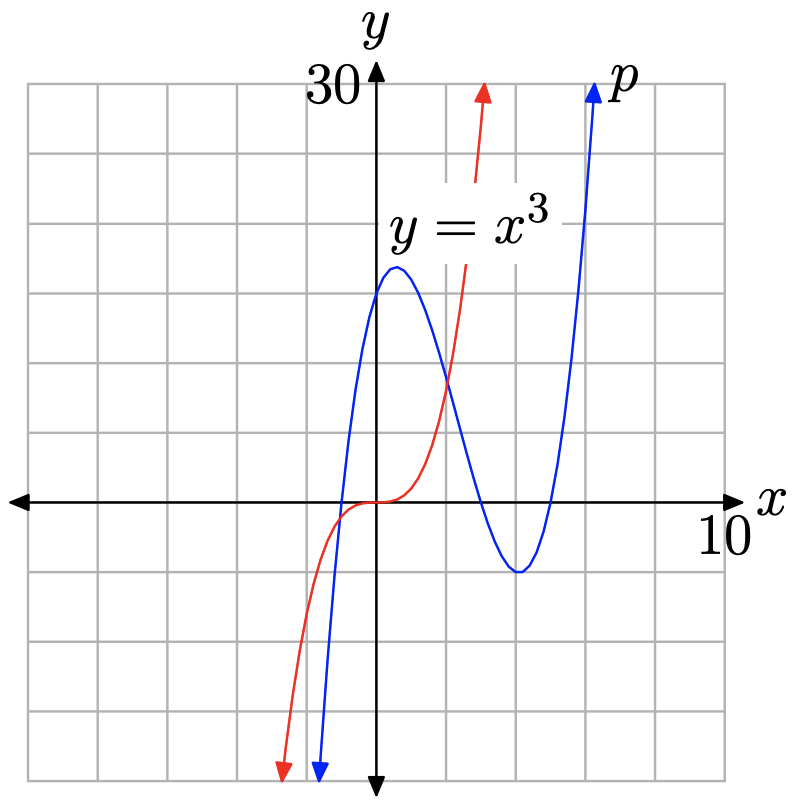
Puede proporcionar una demostración más llamativa de la validez de la afirmación en la ecuación (15) trazando tanto el polinomio p como su término principal (y = x ^ {3} ) en su calculadora, luego alejándose por ajustando los parámetros de la ventana como se muestra en la Figura ( PageIndex {8} ) (b). Observe cómo la gráfica de (p (x) = x ^ {3} -7 x ^ {2} +7 x + 15 ) se parece más a la gráfica de su término principal (y = x ^ {3} ), al menos en los bordes derecho e izquierdo de la ventana de visualización. Cuando nos alejamos más, ajustando los parámetros de la ventana como se muestra en la Figura ( PageIndex {8} ) (d), observe cómo esa gráfica de p se aproxima a la gráfica de su término principal (y = x ^ {3} ) aún más de cerca en cada borde de la ventana de visualización.

Veamos otro ejemplo.
Ejemplo ( PageIndex {6} )
Considere el polinomio [p (x) = – x ^ {4} +37 x ^ {2} +24 x-180 ]. Comente sobre el comportamiento final de p y use su calculadora gráfica para dibujar su gráfica.
Solución
El término principal de (p (x) = – x ^ {4} +37 x ^ {2} +24 x-180 ) es (y = -x ^ {4} ). Conocemos el comportamiento final de la gráfica del término principal. A medida que barremos nuestros ojos de izquierda a derecha, la gráfica de (y = -x ^ {4} ) se eleva desde el infinito negativo, se mueve a través del origen y luego vuelve a disminuir hasta el infinito. La gráfica de p debe exhibir el mismo comportamiento final. De hecho, en la Figura ( PageIndex {9} ), tenga en cuenta que la gráfica de (y = -x ^ {4} ) y (y = -x ^ {4} +37 x ^ {2} + 24 x-180 ) ambos comparten el mismo comportamiento final.
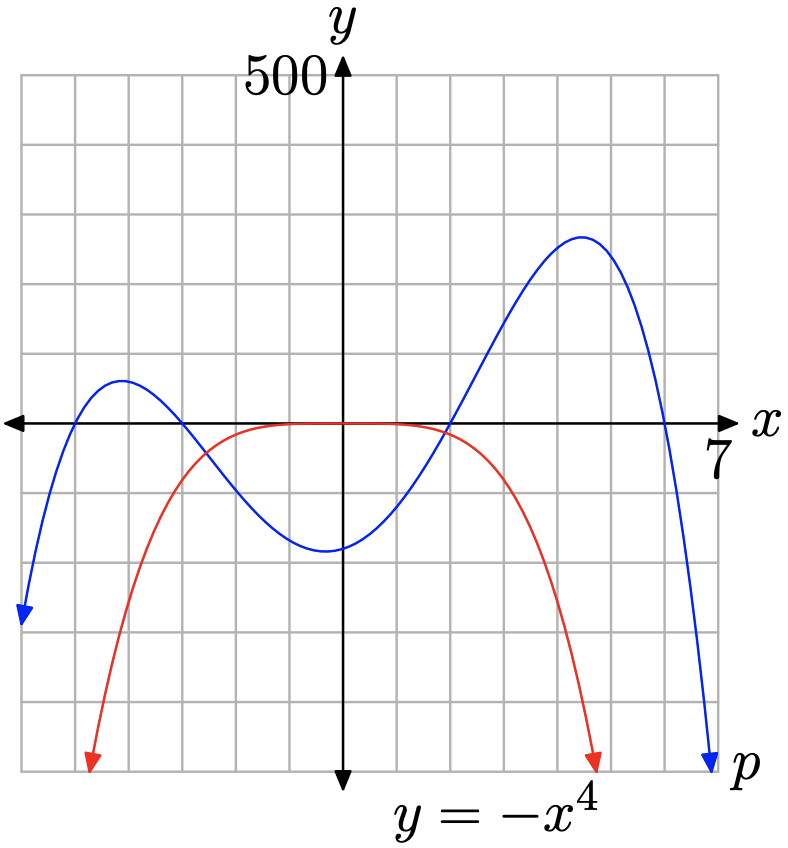
Ejercicio
En Ejercicios 1 – 8 , organice cada polinomio en potencias descendentes de x, establezca el grado del polinomio, identifique el término principal, luego haga una declaración sobre los coeficientes de El polinomio dado.
EJERCICIO ( PageIndex {1} )
(p (x) = 3x − x ^ 2 + 4 − x ^ 3 )
- Respuesta
-
(p (x) = −x ^ 3 − x ^ 2 + 3x + 4 ), grado = 3, término principal = (- x ^ 3 ), “p es un polinomio con coeficientes enteros, polinomio con coeficientes racionales “o” p es
un polinomio con coeficientes reales “.
EJERCICIO ( PageIndex {2} )
(p (x) = 4 + 3x ^ 2−5x + x ^ 3 )
EJERCICIO ( PageIndex {3} )
(p (x) = 3x ^ 2 + x ^ 4 − x − 4 )
- Respuesta
-
(p (x) = x ^ 4 + 3x ^ 2 − x − 4 ), grado = 4, término principal = (x ^ 4 ), “p es un polinomio con coeficientes enteros”, ” p es un polinomio con coeficientes racionales “o” p es
un polinomio con coeficientes reales “.
EJERCICIO ( PageIndex {4} )
(p (x) = −3 + x ^ 2 − x ^ 3 + 5x ^ 4 )
EJERCICIO ( PageIndex {5} )
(p (x) = 5x− frac {3} {2} x ^ 3 + 4− frac {2} {3} x ^ 5 )
- Respuesta
-
(p (x) = – frac {2} {3} x ^ 5− frac {3} {2} x ^ 3 + 5x + 4 ), grado = 5, término inicial = ( – frac {2} {3} x ^ 5 ), “p es un polinomio con coeficientes racionales”, o p es un polinomio con coeficientes reales “.
EJERCICIO ( PageIndex {6} )
(p (x) = – frac {3} {2} x + 5− frac {7} {3} x ^ 5 + frac {4} {3} x ^ 3 ) [19459002 ]
EJERCICIO ( PageIndex {7} )
(p (x) = −x + frac {2} {3} x ^ 3− sqrt {2} x ^ 2 + pi x ^ 6 )
- Respuesta
-
(p (x) = pi x ^ 6 + frac {2} {3} x ^ 3− sqrt {2} x ^ 2 − x ), grado = 6, término inicial = ( pi x ^ 6 ), “p es un polinomio con coeficientes reales”.
EJERCICIO ( PageIndex {8} )
(p (x) = 3+ sqrt {2} x ^ 4 + sqrt {3} x − 2x ^ 2 + sqrt {5} x ^ 6 )
En Ejercicios 9 – 14 , se te presenta la gráfica de (y = ax ^ { n} ) . En cada caso, indique si el grado es par o impar, luego indique si un es un número positivo o negativo.
EJERCICIO ( PageIndex {9} )
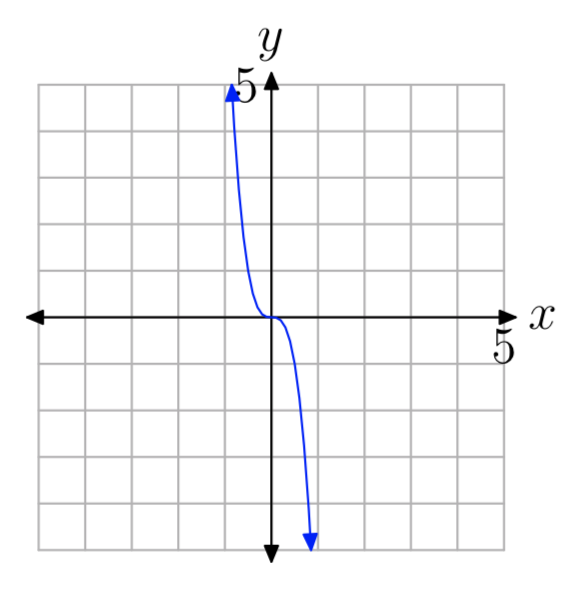
- Respuesta
-
(y = ax ^ {n} ), n impar, a <0.
EJERCICIO ( PageIndex {10} )
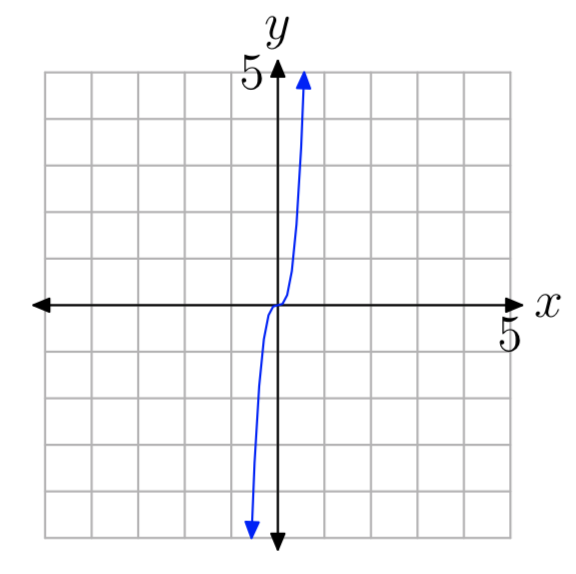
EJERCICIO ( PageIndex {11} )
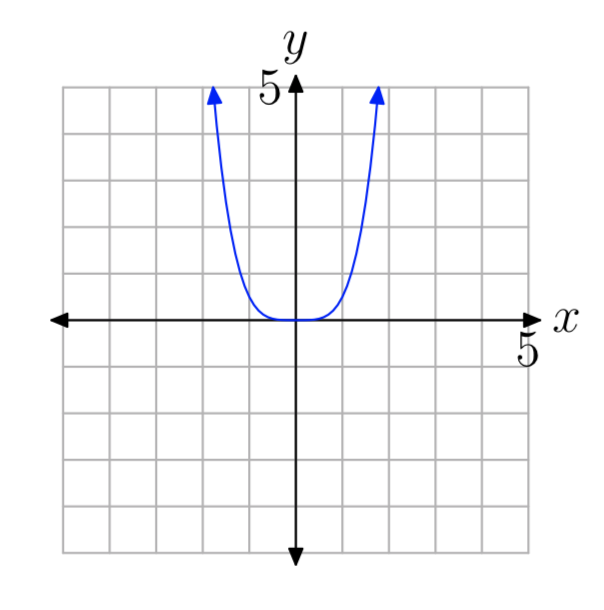
- Respuesta
-
(y = ax ^ {n} ), n par, a> 0.
EJERCICIO ( PageIndex {12} )
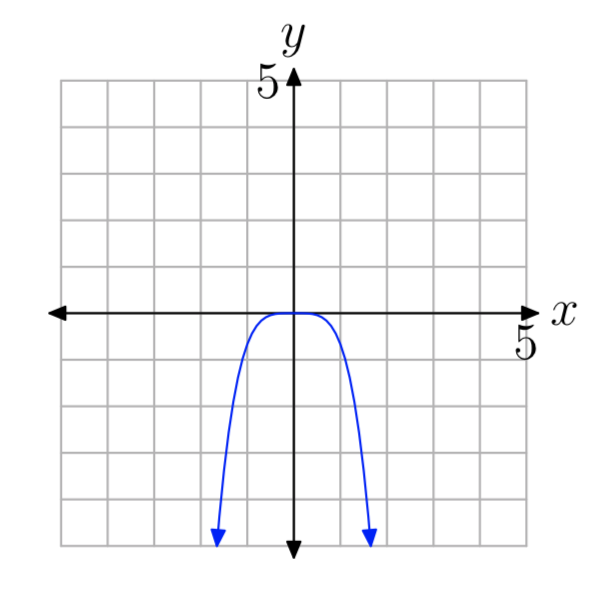
EJERCICIO ( PageIndex {13} )
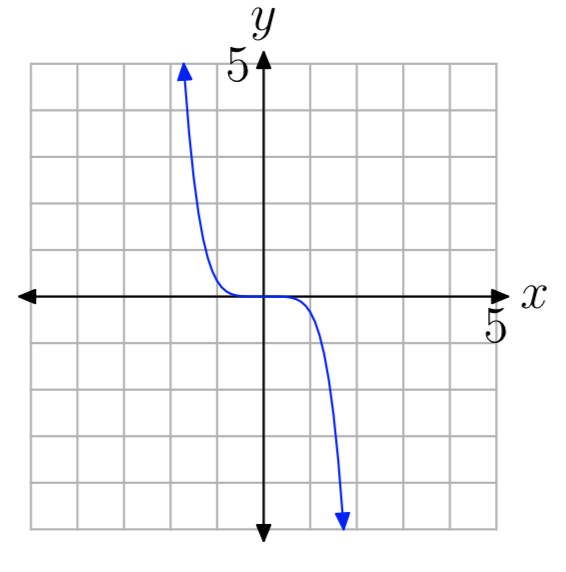
- Respuesta
-
(y = ax ^ {n} ), n impar, a <0.
EJERCICIO ( PageIndex {14} )
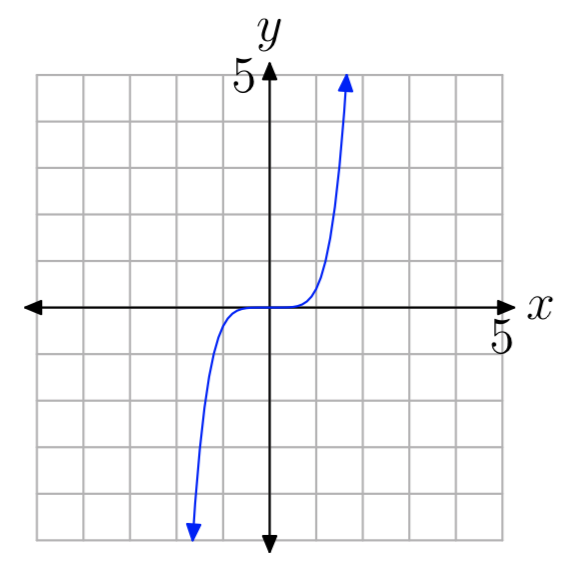
En Ejercicios 15 – 20 , se te presenta la gráfica del polinomio (p (x) = a_ {n} x ^ n + ··· + a_ {1} x + a_ {0} ). En cada caso, indique si el grado del polinomio es par o impar, luego indique si el coeficiente principal an es positivo o negativo.
EJERCICIO ( PageIndex {15} )
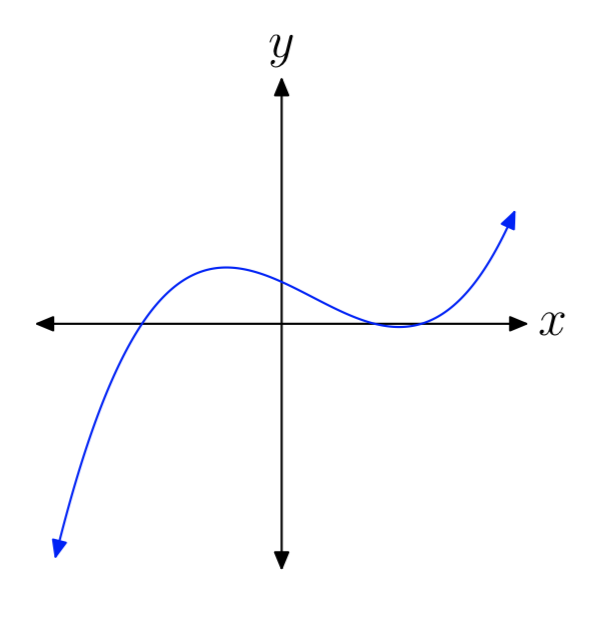
- Respuesta
-
impar, positivo
EJERCICIO ( PageIndex {16} )
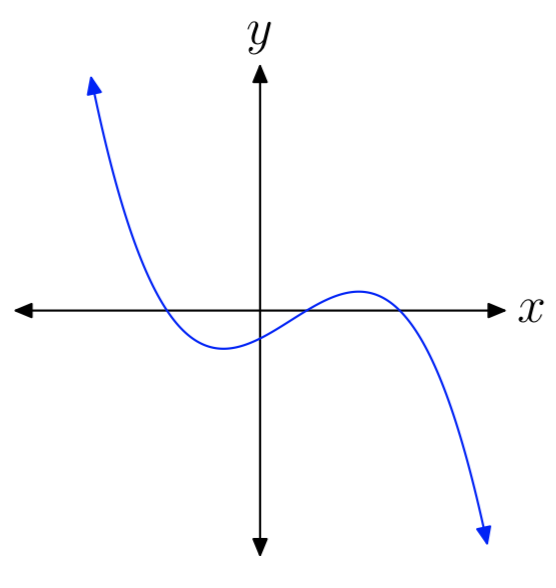
EJERCICIO ( PageIndex {17} )
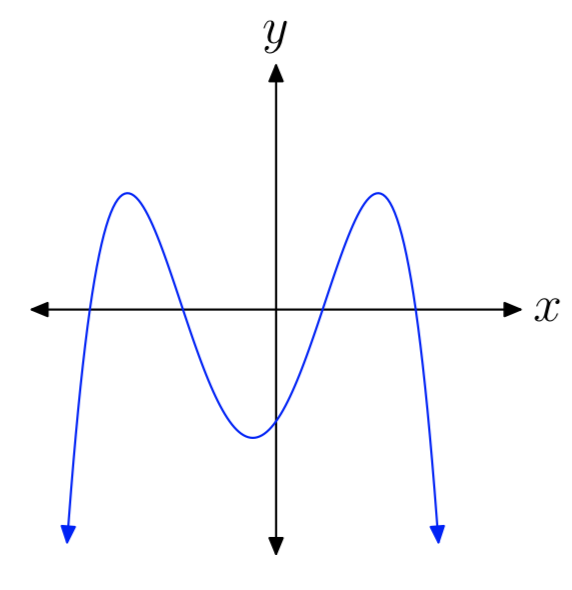
- Respuesta
-
par, negativo
Ejercicio ( PageIndex {18} )
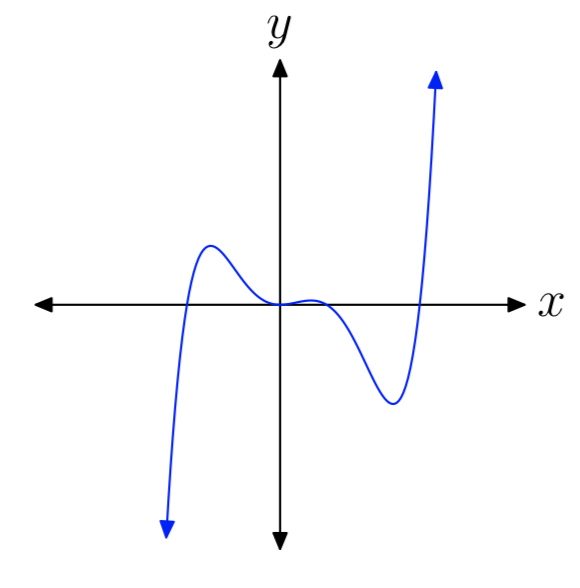
EJERCICIO ( PageIndex {19} )
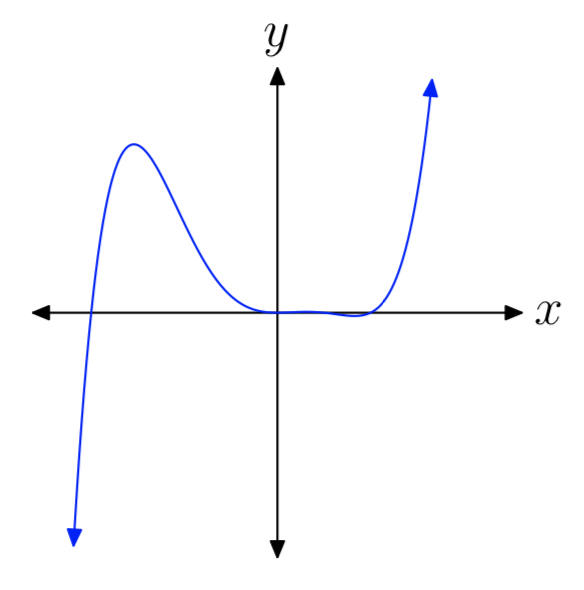
- Respuesta
-
impar, positivo
EJERCICIO ( PageIndex {20} )
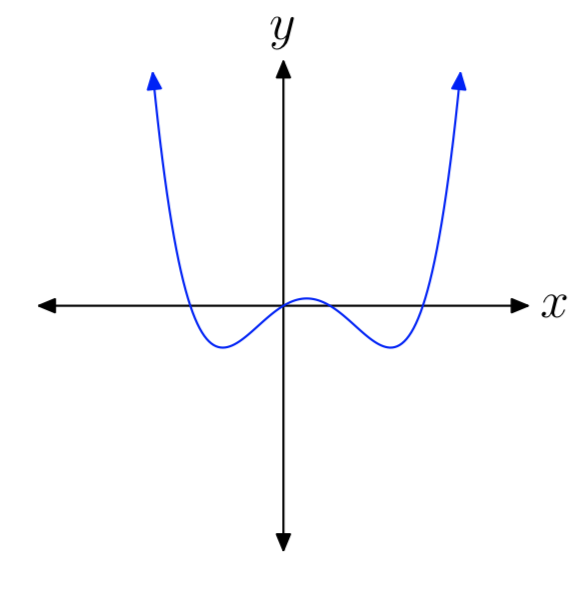
Para cada polinomio en Ejercicios 21 – 30 , realice cada una de las siguientes tareas.
-
Predecir el comportamiento final del polinomio dibujando un boceto muy aproximado del polinomio. Haga esto sin la ayuda de una calculadora. La única preocupación aquí es que su gráfico muestre el comportamiento final correcto.
-
Dibuje el gráfico en su calculadora, ajuste la ventana de visualización para que todos los “puntos de inflexión” del polinomio sean visibles en la ventana de visualización y copie el resultado en su tarea. Como de costumbre, etiquete y escale cada eje con xmin, xmax, ymin e ymax. ¿El comportamiento final real está de acuerdo con su comportamiento final previsto?
EJERCICIO ( PageIndex {21} )
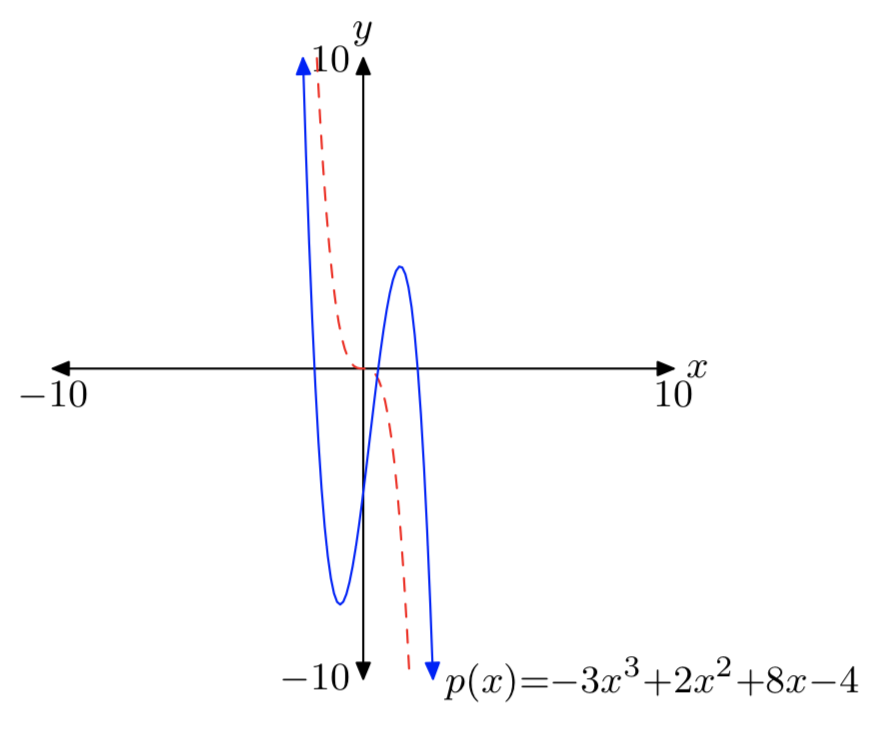
(p (x) = −3x ^ 3 + 2x ^ 2 + 8x − 4 )
- Respuesta
-
Tenga en cuenta que el término principal (- 3x ^ 3 ) (discontinuo) tiene el mismo comportamiento final que el polinomio p.
EJERCICIO ( PageIndex {22} )
(p (x) = 2x ^ 3−3x ^ 2 + 4x − 8 )
EJERCICIO ( PageIndex {23} )
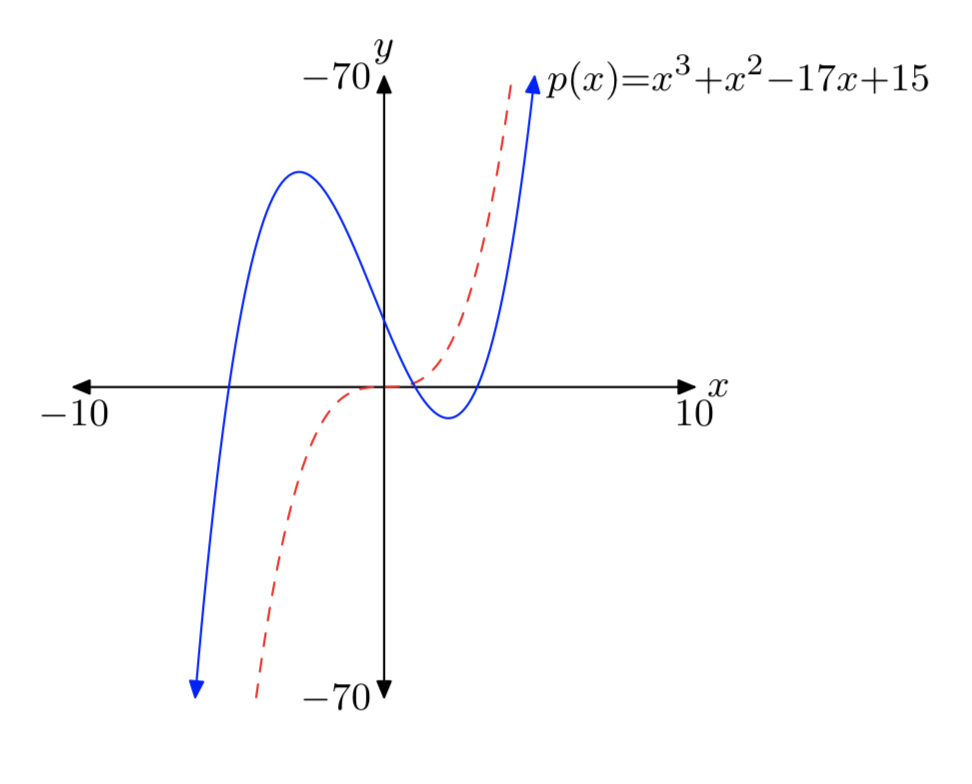
(p (x) = x ^ 3 + x ^ 2−17x + 15 )
- Respuesta
-
Tenga en cuenta que el término principal (x ^ 3 ) (discontinuo) tiene el mismo comportamiento final que el polinomio p.
EJERCICIO ( PageIndex {24} )
(p (x) = −x ^ 4 + 2x ^ 2 + 29x − 30 )
EJERCICIO ( PageIndex {25} )
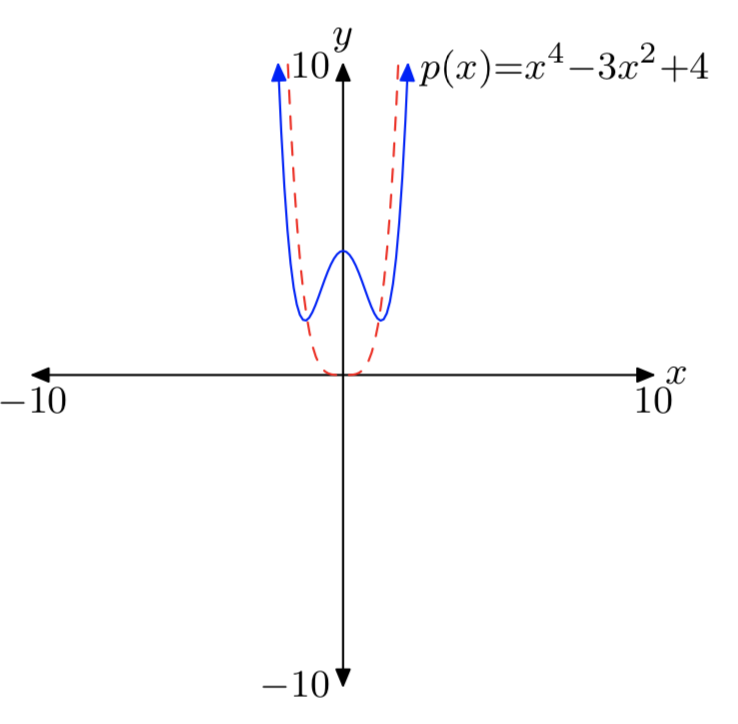
(p (x) = x ^ 4−3x ^ 2 + 4 )
- Respuesta
-
Tenga en cuenta que el término principal (x ^ 4 ) (discontinuo) tiene el mismo comportamiento final que el polinomio p.
EJERCICIO ( PageIndex {26} )
(p (x) = −x ^ 4 + 8x ^ 2−12 )
EJERCICIO ( PageIndex {27} )
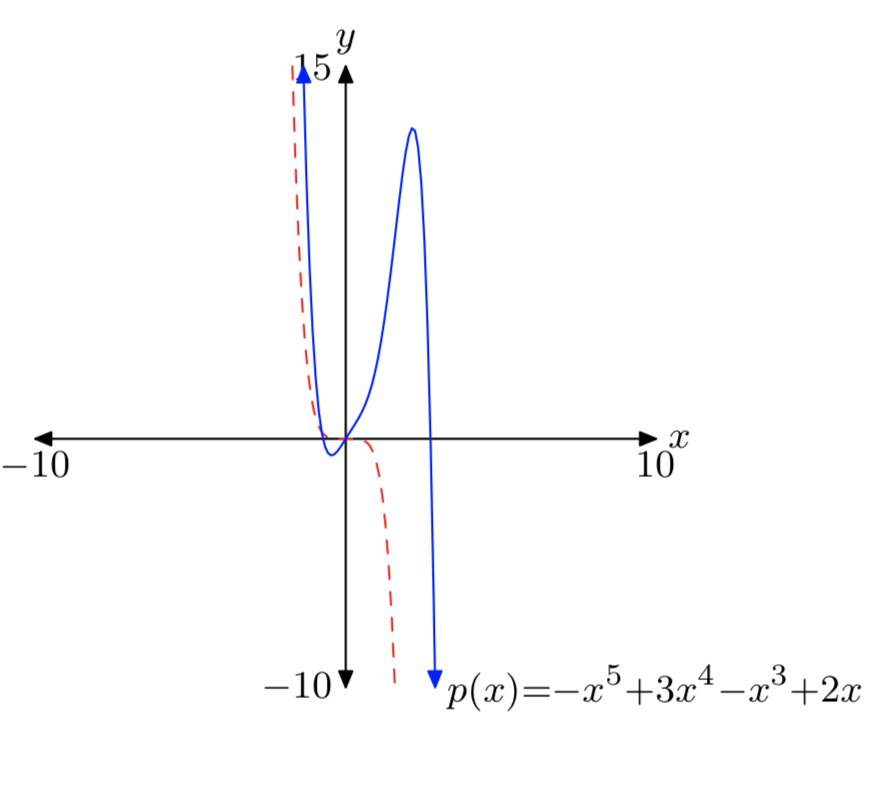
(p (x) = −x ^ 5 + 3x ^ 4 − x ^ 3 + 2x )
- Respuesta
-
Tenga en cuenta que el término principal (- x ^ 5 ) (discontinuo) tiene el mismo comportamiento final que el polinomio p.
EJERCICIO ( PageIndex {28} )
(p (x) = 2x ^ 4−3x ^ 3 + x − 10 )
EJERCICIO ( PageIndex {29} )
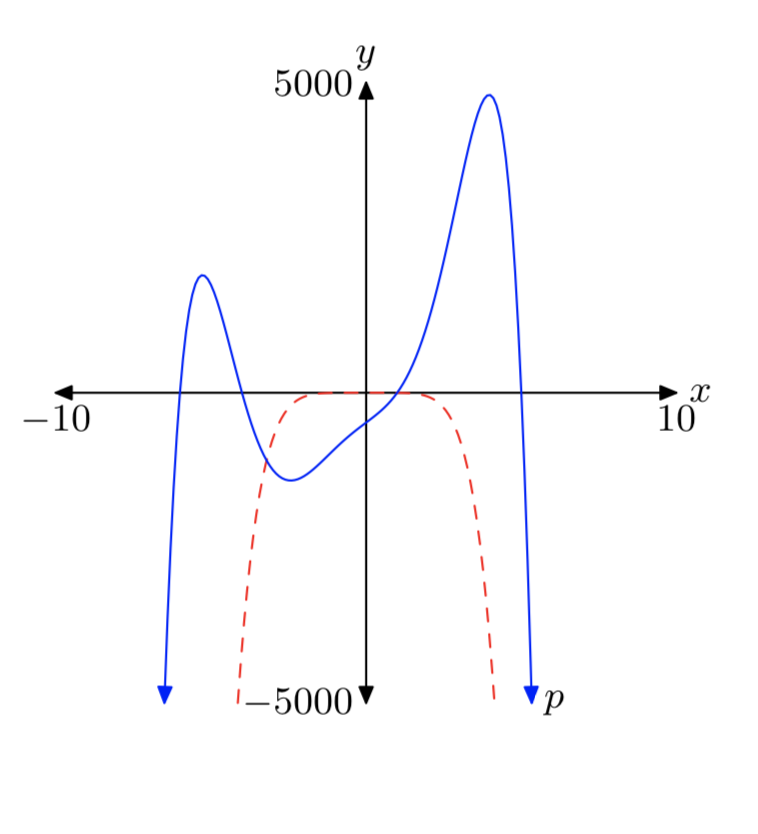
(p (x) = −x ^ 6−4x ^ 5 + 27x ^ 4 + 78x ^ 3 + 4x ^ 2 + 376x − 480 )
- Respuesta
-
Tenga en cuenta que el término principal (- x ^ 6 ) (discontinuo) tiene el mismo comportamiento final que el polinomio p.
EJERCICIO ( PageIndex {30} )
(p (x) = x ^ 5−27x ^ 3 + 30x ^ 2−124x + 120 )
