
Objetivos de aprendizaje
Al final de esta sección, podrá:
- Traducir y resolver ecuaciones porcentuales básicas
- Resolver aplicaciones porcentuales
- Encuentre el porcentaje de aumento y el porcentaje de disminución
- Resolver aplicaciones de interés simple
- Resolver aplicaciones con descuento o recargo
Nota
Antes de comenzar, realiza este cuestionario de preparación.
- Convertir 4.5% a decimal.
Si se perdió este problema, revise [enlace] . - Convertir 0.6 a porcentaje.
Si se perdió este problema, revise [enlace] . - Redondea 0,875 a la centésima más cercana.
Si se perdió este problema, revise [enlace] . - Multiplicar (4.5) (2.38).
Si se perdió este problema, revise [enlace] . - Resuelve 3.5 = 0.7n.
Si se perdió este problema, revise [enlace] . - Restar 50−37.45.
Si se perdió este problema, revise [enlace] .
Traducir y resolver ecuaciones porcentuales básicas
Resolveremos ecuaciones porcentuales usando los métodos que usamos para resolver ecuaciones con fracciones o decimales. Sin las herramientas de álgebra, el mejor método disponible para resolver problemas porcentuales era establecerlos como proporciones. Ahora, como estudiante de álgebra, puedes traducir oraciones en inglés a ecuaciones algebraicas y luego resolver las ecuaciones.
Podemos usar cualquier letra que desee como variable, pero es una buena idea elegir una letra que nos recuerde lo que está buscando. Debemos asegurarnos de cambiar el porcentaje dado a un decimal cuando lo ponemos en la ecuación.
Ejercicio ( PageIndex {1} )
Traducir y resolver: ¿Qué número es 35% de 90?
- Respuesta
-
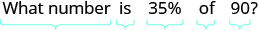
Traducir al álgebra. Deje n = el número. 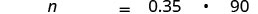
Recuerde que “de” significa multiplicar, “es” significa igual. Multiplica. 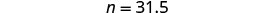
31.5 es 35% de 90
Ejercicio ( PageIndex {2} )
Traducir y resolver:
¿Qué número es 45% de 80?
- Respuesta
-
36
Ejercicio ( PageIndex {3} )
Traducir y resolver:
¿Qué número es 55% de 60?
- Respuesta
-
33
Debemos tener mucho cuidado cuando traducimos las palabras en el siguiente ejemplo. La cantidad desconocida no se aislará al principio, como lo fue en Ejemplo . Nuevamente usaremos la traducción directa para escribir la ecuación.
Ejercicio ( PageIndex {4} )
Traducir y resolver: ¿6.5% de qué número es $ 1.17?
- Respuesta
-

Traducir. Deje n = el número. 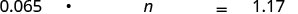
Multiplica. 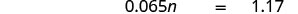
Divide ambos lados entre 0.065 y simplifica. 
6.5% de $ 18 es $ 1.17
Ejercicio ( PageIndex {5} )
Traducir y resolver:
¿7.5% de qué número es $ 1.95?
- Respuesta
-
$ 26
Ejercicio ( PageIndex {6} )
Traducir y resolver:
8.5% de qué número es $ 3.06?
- Respuesta
-
$ 36
En el siguiente ejemplo, estamos buscando el porcentaje.
Ejercicio ( PageIndex {7} )
Traducir y resolver: 144 es qué porcentaje de 96?
- Respuesta
-
Tenga en cuenta que se nos pide encontrar el porcentaje, por lo que debemos tener nuestro resultado final en forma de porcentaje.
Ejercicio ( PageIndex {8} )
Traducir y resolver:
110 es cuántos por ciento de 88?
- Respuesta
-
125%
Ejercicio ( PageIndex {9} )
Traducir y resolver:
126 es cuántos por ciento de 72?
- Respuesta
-
175%
Resolver aplicaciones de porcentaje
Muchas aplicaciones del por ciento , como propinas, impuestos sobre las ventas, descuentos e intereses, ocurren en nuestra vida diaria. Para resolver estas aplicaciones, traduciremos a una ecuación porcentual básica, como las que resolvimos en ejemplos anteriores. Una vez que traducimos la oración en una ecuación porcentual, sabemos cómo resolverla.
Replantearemos la estrategia de resolución de problemas que utilizamos anteriormente para facilitar la referencia.
USE UNA ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS PARA SOLUCIONAR UNA APLICACIÓN.
- Lea el problema. Asegúrese de que se entiendan todas las palabras e ideas.
- Identifique lo que estamos buscando.
- Nombre lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traduzca en una ecuación. Puede ser útil repetir el problema en una oración con toda la información importante. Luego, traduce la oración en inglés a una ecuación algebraica.
- Resuelve la ecuación usando buenas técnicas de álgebra.
- Marque la respuesta en el problema y asegúrese de que tenga sentido.
- Respuesta la pregunta con una oración completa.
Ahora que tenemos la estrategia de referencia y hemos practicado la resolución de ecuaciones porcentuales básicas, estamos listos para resolver aplicaciones porcentuales. Asegúrese de preguntarse si su respuesta final tiene sentido, ya que muchas de las aplicaciones involucrarán situaciones cotidianas, puede confiar en su propia experiencia.
Ejercicio ( PageIndex {10} )
Dezohn y su novia disfrutaron de una buena cena en un restaurante y su factura fue de $ 68.50. Quiere dejar una propina del 18%. Si la propina será el 18% de la factura total, ¿cuánta propina debería dejar?
- Respuesta
-
Observe que usamos t para representar la punta desconocida.Paso 1. Lea el problema. Paso 2. Identifique lo que estamos buscando. la cantidad de propina que debería dejar Dezohn Paso 3. Nombre lo que estamos buscando. Elija una variable para representarla. Sea t = cantidad de propina. Paso 4. Traduzca en una ecuación. 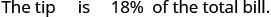
Escribe una oración que proporcione la información para encontrarla. 
Traduce la oración a una ecuación. 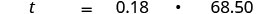
Paso 5. Resuelve la ecuación. Multiplicar. 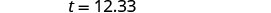
Paso 6. Verificar. ¿Tiene sentido? Sí, el 20% de $ 70 es $ 14. Paso 7. Responda la pregunta con una oración completa. Dezohn debería dejar una propina de $ 12.33.
Ejercicio ( PageIndex {11} )
Cierra y su hermana disfrutaron de una cena en un restaurante y la factura fue de $ 81.50. Si quiere dejar el 18% de la factura total como propina, ¿cuánto debería dejar?
- Respuesta
-
$ 14,67
Ejercicio ( PageIndex {12} )
Kimngoc almorzó en su restaurante favorito. Ella quiere dejar el 15% de la factura total como su propina. Si su factura fue de $ 14.40, ¿cuánto dejará para la propina?
- Respuesta
-
$ 2,16
Ejercicio ( PageIndex {13} )
La etiqueta del cereal de desayuno de Masao decía que una porción de cereal proporciona 85 miligramos (mg) de potasio, que es el 2% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de potasio?
- Respuesta
-
Paso 1. Lea el problema. Paso 2. Identifique lo que estamos buscando. la cantidad total de potasio que se recomienda Paso 3. Nombre lo que estamos buscando. Elija una variable para representarla. Sea a = cantidad total de potasio. Paso 4. Traducir. Escribe una oración que brinde la información para encontrarla. 
Traducir a una ecuación. 
Paso 5. Resuelve la ecuación. 
Paso 6. Verificar. ¿Tiene sentido? Sí, 2% es un pequeño porcentaje y 85 es una pequeña parte de 4,250. Paso 7. Responda la pregunta con una oración completa. La cantidad de potasio que se recomienda es de 4.250 mg.
Ejercicio ( PageIndex {14} )
Una porción de cereal cuadrado de trigo tiene siete gramos de fibra, que es el 28% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria recomendada total de fibra?
- Respuesta
-
25 gramos
Ejercicio ( PageIndex {15} )
Una porción de cereal de arroz tiene 190 mg de sodio, que es el 8% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de sodio?
- Respuesta
-
2,375 mg
Ejercicio ( PageIndex {16} )
Mitzi recibió algunos brownies gourmet como regalo. La envoltura dijo que cada brownie tenía 480 calorías y 240 calorías de grasa. ¿Qué porcentaje del total de calorías en cada brownie proviene de la grasa?
- Respuesta
Ejercicio ( PageIndex {17} )
Resolver. Redondea al porcentaje entero más cercano.
Veronica planea hacer muffins de una mezcla. El paquete dice que cada panecillo tendrá 230 calorías y 60 calorías serán de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa?
- Respuesta
-
26%
Ejercicio ( PageIndex {18} )
Resolver. Redondea al porcentaje entero más cercano.
La mezcla que Ricardo planea usar para hacer brownies dice que cada brownie tendrá 190 calorías, y 76 calorías son de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa?
- Respuesta
-
40%
Encuentre el porcentaje de aumento y el porcentaje de disminución
La gente en los medios de comunicación a menudo habla sobre cuánto ha aumentado o disminuido una cantidad durante un cierto período de tiempo. Por lo general, expresan este aumento o disminución como un porcentaje.
Para encontrar el aumento porcentual , primero encontramos la cantidad de aumento, la diferencia de la nueva cantidad y la cantidad original. Luego encontramos qué porcentaje es la cantidad de aumento de la cantidad original.
ENCUENTRE EL INCREMENTO POR CIENTO.
- Encuentra la cantidad de aumento.
( text {nueva cantidad} – text {cantidad original} = text {aumentar} )
- Encuentre el porcentaje de aumento.
¿El aumento es qué porcentaje de la cantidad original?
Ejercicio ( PageIndex {19} )
En 2011, el gobernador de California propuso aumentar las tarifas de los colegios comunitarios de $ 26 por unidad a $ 36 por unidad. Encuentra el porcentaje de aumento. (Redondear a la décima de porcentaje más cercana)
- Respuesta
Ejercicio ( PageIndex {20} )
Halla el porcentaje de aumento. (Redondear a la décima de porcentaje más cercana)
En 2011, el IRS aumentó el costo del kilometraje deducible a 55,5 centavos de dólar desde 51 centavos.
- Respuesta
-
8,8%
Ejercicio ( PageIndex {21} )
Halla el porcentaje de aumento.
En 1995, la tarifa estándar de autobús en Chicago era de $ 1.50. En 2008, la tarifa estándar del autobús era de $ 2.25.
- Respuesta
-
50%
Encontrar el porcentaje de disminución es muy similar a encontrar el porcentaje de aumento, pero ahora la cantidad de disminución es la diferencia entre la cantidad original y la nueva cantidad. Luego encontramos qué porcentaje es la cantidad de disminución de la cantidad original.
ENCUENTRE EL PORCENTAJE DE DISMINUCIÓN.
- Encuentra la cantidad de disminución.
( text {cantidad original} – text {nueva cantidad} = text {disminuir} )
- Halla el porcentaje de disminución.
La disminución es ¿qué porcentaje de la cantidad original?
Ejercicio ( PageIndex {22} )
El precio promedio de un galón de gasolina en una ciudad en junio de 2014 fue de $ 3.71. El precio promedio en esa ciudad en julio fue de $ 3.64. Encuentra el porcentaje de disminución.
- Respuesta
Ejercicio ( PageIndex {23} )
Halla el porcentaje de disminución. (Redondear a la décima de porcentaje más cercana)
La población de Dakota del Norte era de aproximadamente 672,000 en 2010. Se prevé que la población sea de aproximadamente 630,000 en 2020.
- Respuesta
-
6,3%
Ejercicio ( PageIndex {24} )
Halla el porcentaje de disminución.
El año pasado, el salario de Sheila fue de $ 42,000. Debido a los días de licencia, este año, su salario fue de $ 37,800.
- Respuesta
-
10%
Resolver aplicaciones de interés simple
¿Sabes que los bancos te pagan para conservar tu dinero? El dinero que un cliente pone en el banco se llama principal , P , y el dinero que el banco paga al cliente se llama interés . El interés se calcula como un cierto porcentaje del principal; llamado la tasa de interés , r . Por lo general, expresamos la tasa de interés como porcentaje por año, y la calculamos usando el equivalente decimal del porcentaje. La variable t , (por tiempo ) representa el número de años que el dinero está en la cuenta.
Para encontrar el interés, utilizamos la fórmula de interés simple, I = Prt.
INTERÉS SIMPLE
Si una cantidad de dinero, P , llamada principal, se invierte por un período de t años a una tasa de interés anual r , la cantidad de interés, I , obtenido es
[ begin {array} {lllll} {} & {} & {I} & {=} & { text {interés}} \ {I = Prt} & { text {where}} & {P} & {=} & { text {principio}} \ {} & {} & {r} & {=} y { text {rate}} \ {} & {} & {t} & {=} & { text {time}} end {array} ]
El interés ganado de acuerdo con esta fórmula se llama interés simple .
El interés también se puede calcular de otra manera, llamada interés compuesto. Este tipo de interés se cubrirá en clases de matemáticas posteriores.
La fórmula que usamos para calcular el interés simple es I = Prt. Para usar la fórmula, sustituimos en los valores que el problema nos da las variables y luego resolvemos la variable desconocida. Puede ser útil organizar la información en un cuadro.
Ejercicio ( PageIndex {25} )
Nathaly depositó $ 12,500 en su cuenta bancaria donde ganará un 4% de interés. ¿Cuánto interés ganará Nathaly en 5 años?
[ begin {alineado} I & =? \ P & = $ 12,500 \ r & = 4 % \ t & = 5 text {años} end {alineado} ]
- Respuesta
-
( begin {array} {ll} { textbf {Paso 1. Leer} text {el problema.}} & {} \ \ { textbf {Paso 2. Identificar} text {what estamos buscando.}} & { text {la cantidad de intereses ganados}} \\ { textbf {Paso 3. Nombre} text {lo que estamos buscando.}} & { text {Let I = la cantidad de interés.}} \ { text {Elija una variable para representar esa cantidad}} & { text {}} \\ { textbf {Paso 4.} text {Traducir a una ecuación. }} & {} \ { qquad text {Escriba la fórmula.}} & {I = Prt} \ { qquad text {Sustituya la información dada.}} & {I = (12500) (. 04) (5)} \ \ { textbf {Paso 5. Resuelva} text {la ecuación.}} & {I = 2500} \ \ { textbf {Paso 6. Verifique} text {: ¿Tiene sentido?}} & {} \\ { qquad text {Is} $ 2,500 text {es un interés razonable}} & {} \ { qquad text {on} $ 12,500? Text { Sí.}} \ { textbf {Paso 7. Responde} text {la pregunta con un}} y { text {El interés es} $ 2500} \ { text {oración completa.}} & {} end {array} )
Ejercicio ( PageIndex {26} )
Areli invirtió un capital de $ 950 en su cuenta bancaria con una tasa de interés del 3%. ¿Cuánto interés ganó en 5 años?
- Respuesta
-
$ 142.50
Ejercicio ( PageIndex {27} )
Susana invirtió un capital de $ 36,000 en su cuenta bancaria con una tasa de interés del 6.5%. ¿Cuánto interés ganó en 3 años?
- Respuesta
-
$ 7020
Puede haber ocasiones en las que sepamos la cantidad de intereses devengados sobre un capital determinado durante un período de tiempo determinado, pero no sabemos la tasa. Para encontrar la tasa, utilizamos la fórmula de interés simple, sustituimos en los valores dados el principal y el tiempo, y luego resolvemos la tasa.
Ejercicio ( PageIndex {28} )
Loren le prestó a su hermano $ 3,000 para ayudarlo a comprar un automóvil. En 4 años, su hermano le devolvió los $ 3,000 más $ 660 en intereses. ¿Cuál fue la tasa de interés?
[ begin {array} {lll} {I} & {=} & { $ 660} \ {P} & {=} & { $ 3000} \ {r} & {=} & {?} \ {t} & {=} & {4 text {años}} end {array} ]
- Respuesta
-
( begin {array} {ll} { textbf {Paso 1. Leer} text {el problema.}} & {} \ \ { textbf {Paso 2. Identificar} text {what estamos buscando.}} & { text {la tasa de interés}} \\ { textbf {Paso 3. Nombre} text {lo que estamos buscando. Elija}} & { text {Let r = la tasa de interés.}} \ { text {una variable para representar esa cantidad}} & { text {}} \\ { textbf {Paso 4.} text {Traducir a una ecuación.} } & {} \ { qquad text {Escriba la fórmula.}} & {I = Prt} \ { qquad text {Sustituya la información dada.}} & {660 = (3000) r (4 )} \ \ { textbf {Paso 5. Resolver} text {la ecuación.}} & {} \ {} & {660 = (12000) r} \ { text {Divide.}} & {0.055 = r} \ { text {Cambiar a forma de porcentaje.}} & {5.5 % = r} \\ { textbf {Paso 6. Marque} text {: ¿Tiene sentido?}} & {} \\ {I = Prt} & {} \ {660 stackrel {?} {=} (3000) (0.055) (4)} & {} \ {660 = 660 marca de verificación} & {} \ { textbf {Paso 7. Contestar} text {la pregunta con}} y { text {La tasa de interés fue} 5.5%} \ { text {oración completa.}} & {} end {arra y} )
Observe que, en este ejemplo, el hermano de Loren le pagó intereses a Loren, tal como lo hubiera hecho un banco si Loren hubiera invertido su dinero allí.
Ejercicio ( PageIndex {29} )
Jim le prestó a su hermana $ 5,000 para ayudarla a comprar una casa. En 3 años, ella le pagó los $ 5,000, más $ 900 de interés. ¿Cuál fue la tasa de interés?
- Respuesta
-
6%
Ejercicio ( PageIndex {30} )
Hang pidió prestados $ 7,500 de sus padres para pagar su matrícula. En 5 años, ella les pagó $ 1,500 de interés además de los $ 7,500 que pidió prestados. ¿Cuál fue la tasa de interés?
- Respuesta
-
4%
Ejercicio ( PageIndex {31} )
Eduardo notó que sus documentos de préstamos para automóviles nuevos indicaban que con una tasa de interés del 7.5%, pagaría $ 6,596.25 en intereses durante 5 años. ¿Cuánto pidió prestado para pagar su auto?
- Respuesta
-
( begin {array} {ll} { textbf {Paso 1. Leer} text {el problema.}} & {} \ \ { textbf {Paso 2. Identificar} text {what estamos buscando.}} & { text {la cantidad prestada (el principal)}} \ { text {una variable para representar esa cantidad.}} & {} \\ { textbf {Paso 3. Nombre} text {lo que estamos buscando.}} & { Text {Let P = principal prestado.}} \ { text {Elija una variable para representar esa cantidad}} & { text {}} \ \ { textbf {Paso 4. Traducir} text {en una ecuación.}} & {} \ { qquad text {Escriba la fórmula.}} & {I = Prt} \ { qquad text {Sustituya en la información dada.}} & {6596.25 = P (0.075) (5)} \ \ { textbf {Paso 5. Resuelva} text {la ecuación.}} & {} \ {} & {6596.25 = 0.375P} \ { text {Divide.}} & {17590 = P} \ \ { textbf {Paso 6. Marque} text {: ¿Tiene sentido?}} & {} {I = Prt} & {} \ {6596.25 stackrel {?} {=} (17590) (0.075) (5)} & {} \ {6596.25 = 6596.25 checkmark} & {} \\ { textbf {Paso 7. Respuesta} text {la pregunta con un}} & { text {El principal es} $ 17590} \ { text { oración completa.}} & {} end {array} )
Ejercicio ( PageIndex {32} )
El nuevo estado de préstamo de Sean dijo que pagaría $ 4,866.25 en intereses de una tasa de interés del 8.5% durante 5 años. ¿Cuánto pidió prestado para comprar su auto nuevo?
- Respuesta
-
$ 11,450
Ejercicio ( PageIndex {33} )
En 5 años, la cuenta bancaria de Gloria ganó $ 2,400 de interés al 5%. ¿Cuánto había depositado en la cuenta?
- Respuesta
-
$ 9,600
Resolver aplicaciones con descuento o recargo
Las aplicaciones de descuento son muy comunes en entornos minoristas. Cuando compra un artículo en oferta, el precio original se descuenta por una cantidad en dólares. La tasa de descuento , generalmente dada como un porcentaje, se usa para determinar el monto del descuento. Para determinar la cantidad de descuento , multiplicamos la tasa de descuento por el precio original.
Resumimos el modelo de descuento en el cuadro a continuación.
DESCUENTO
[ begin {array} {l} { text {cantidad de descuento} = text {tasa de descuento} times text {precio original}} \ { text {precio de venta} = text { precio original – cantidad de descuento}} end {array} ]
Tenga en cuenta que el precio de venta siempre debe ser inferior al precio original.
Ejercicio ( PageIndex {34} )
Elise compró un vestido que tenía un descuento del 35% del precio original de $ 140. ¿Cuál fue ⓐ la cantidad de descuento y ⓑ el precio de venta del vestido?
- Respuesta
-
1. ( begin {array} {lll} { text {Precio original}} & {=} y {$ 140} \ { text {Tasa de descuento}} & {=} & {35 % } \ { text {Discount?}} & {=} & {?} end {array} )
( begin {array} {ll} \ { textbf {Paso 1. Leer} text {el problema.}} & {} \ \ { textbf {Paso 2. Identificar} text {lo que estamos buscando.}} & { text {la cantidad de descuento}} \\ { textbf {Paso 3. Nombre} text {lo que estamos buscando.}} & { text {}} \ { text {Elija una variable para representar esa cantidad.}} & { text {Sea d = la cantidad de descuento.}} \\ { textbf {Paso 4. Traduzca} text {en una ecuación. Escriba una oración}} & {} \ { text {que proporcione la información para encontrarla. }} & {} \ { text {Traducir a una ecuación}} & {d = 0.35 (140)} \ \ { textbf {Paso 5. Resolver} text {la ecuación.}} & {d = 49} \ \ { textbf {Paso 6. Verificar} text {: ¿Tiene sentido?}} & {} \ \ { text {Es un} $ 49 text {descuento razonable para un} } & {} \ {$ 140 text {vestido? Sí.}} & {} \\ { textbf {Paso 7. Escribe} text {una oración completa para responder}} & { text {El monto del descuento fue} $ 49} \ { text {la pregunta.}} & {} end {array} )2.
Lea el problema nuevamente.Paso 1. Identifique lo que estamos buscando. el precio de venta del vestido Paso 2. Nombre lo que estamos buscando. Elija una variable para representar esa cantidad. Sea s = el precio de venta. Paso 3. Traduzca en una ecuación. Escribe una oración que proporcione la información para encontrarla. 
Traducir a una ecuación. 
Paso 4. Resuelve la ecuación. 
Paso 5. Verificar. ¿Tiene sentido? ¿El precio de venta es menor que el precio original? Sí, $ 91 es menos de $ 140. Paso 6. Responda la pregunta con una oración completa. El precio de venta del vestido fue de $ 91.
Ejercicio ( PageIndex {35} )
Encuentre ⓐ la cantidad de descuento y ⓑ el precio de venta:
Sergio compró un cinturón con un descuento del 40% de un precio original de $ 29.
- Respuesta
-
ⓐ $ 11.60 ⓑ $ 17.40
Ejercicio ( PageIndex {36} )
Encuentre ⓐ la cantidad de descuento y ⓑ el precio de venta:
Oscar compró una barbacoa que tenía un descuento del 65% de un precio original de $ 395.
- Respuesta
-
256 $ 256,75 ⓑ $ 138,25
Puede haber ocasiones en que sepamos el precio original y el precio de venta, y queremos saber la tasa de descuento . Para encontrar la tasa de descuento, primero encontraremos la cantidad de descuento y luego la usaremos para calcular la tasa como un porcentaje del precio original. El ejercicio ( PageIndex {37} ) mostrará este caso.
Ejercicio ( PageIndex {37} )
Jeannette compró un traje de baño a un precio de venta de $ 13.95. El precio original del traje de baño era de $ 31. Encuentre la cantidad de descuento y la tasa de descuento.
- Respuesta
-
ⓐ ( begin {array} {lll} { text {Precio original}} & {=} y {$ 31} \ { text {Discount}} & {=} & {?} \ { text {Precio de venta}} & {=} y {$ 13.95} end {array} )
( begin {array} {ll} \ { textbf {Paso 1. Leer} text { el problema.}} & {} \ \ { textbf {Paso 2. Identificar} text {lo que estamos buscando.}} & { text {la cantidad de descuento}} \\ { textbf {Paso 3. Nombre} text {lo que estamos buscando.}} & { Text {}} \ { text {Elija una variable para representar esa cantidad.}} & { Text {Sea d = la cantidad de descuento.}} \\ { textbf {Paso 4. Traducir} text {en una ecuación. Escriba una}} & {} \ { text {oración que proporcione la información para encontrarla.}} & { text {El descuento es la diferencia entre el original}} \ {} & { text {precio y el precio de venta.}} \ { text {Traducir a una ecuación}} & {d = 31 – 13.95 } \ \ { textbf {Paso 5. Resolver} text {la ecuación.}} & {d = 17.05} \ \ { textbf {Paso 6. Marque} text {: ¿Tiene sentido? }} & {} \ \ { text {Is} 17.05 text {menor que 31? Sí.}} & {} \\ { te xtbf {Paso 7. Respuesta} text {la pregunta con una oración completa.}} & { text {El monto del descuento fue} $ 17.05} end {array} )ⓑ
Lea el problema nuevamente.
Ejercicio ( PageIndex {38} )
Buscar
- la cantidad de descuento y
- la tasa de descuento.
Lena compró una mesa de cocina al precio de venta de $ 375.20. El precio original de la mesa era de $ 560.
- Respuesta
-
- $ 184.80
- 33%
Ejercicio ( PageIndex {39} )
Buscar
- la cantidad de descuento y
- la tasa de descuento.
Nick compró un aire acondicionado para varias habitaciones a un precio de venta de $ 340. El precio original del aire acondicionado era de $ 400.
- Respuesta
-
- $ 60
- 15%
Las aplicaciones de marcado son muy comunes en entornos minoristas. El precio que un minorista paga por un artículo se llama el costo original . Luego, el minorista agrega un recargo al costo original para obtener el precio de lista , el precio por el que vende el artículo. El recargo generalmente se calcula como un porcentaje del costo original. Para determinar la cantidad de margen, multiplique la tasa de margen por el costo original.
Resumimos el modelo de marcado en el cuadro a continuación.
MARK-UP
[ begin {array} {l} { text {cantidad de margen} = text {tasa de margen} times text {costo original}} \ { text {precio de lista} = text {costo original} + text {cantidad de margen}} end {array} ]
Tenga en cuenta que el precio de lista siempre debe ser superior al costo original.
Ejercicio ( PageIndex {41} )
Buscar
- la cantidad de margen y
- el precio de lista.
La tienda de música de Jim compró una guitarra al costo original de $ 1,200. Jim marcó el precio hasta un 50%.
- Respuesta
-
- $ 600
- $ 1,800
Ejercicio ( PageIndex {42} )
Buscar
- la cantidad de margen y
- el precio de lista.
La tienda de reventa automática compró el Toyota de Pablo por $ 8,500. Marcaron el precio hasta un 35%.
- Respuesta
-
- $ 2,975
- $ 11,475
Glosario
- cantidad de descuento
- La cantidad de descuento es la cantidad resultante cuando una tasa de descuento se multiplica por el precio original de un artículo.
- tasa de descuento
- La tasa de descuento es el porcentaje utilizado para determinar la cantidad de un descuento, común en entornos minoristas.
- interés
- El interés es el dinero que un banco paga a sus clientes por mantener su dinero en el banco.
- precio de lista
- El precio de lista es el precio por el que un minorista vende un artículo.
- marcado
- Un margen de beneficio es un porcentaje del costo original utilizado para aumentar el precio de un artículo.
- costo original
- El costo original en un entorno minorista es el precio que un minorista paga por un artículo.
- director
- El principal es la cantidad original de dinero invertido o prestado por un período de tiempo a una tasa de interés específica.
- tasa de interés
- La tasa de interés es un porcentaje del capital, generalmente expresado como un porcentaje por año.
- interés simple
- El interés simple es el interés ganado de acuerdo con la fórmula I = Prt.
