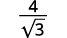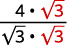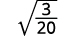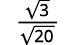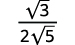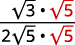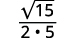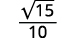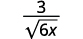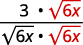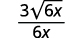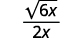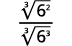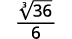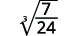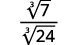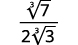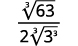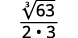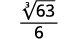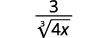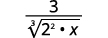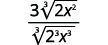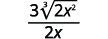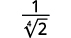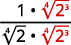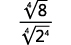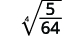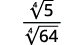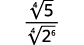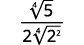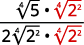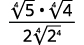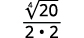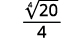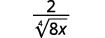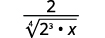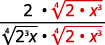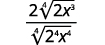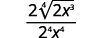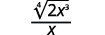Saltar al contenido
las matematicas
radicales

8.6: Dividir expresiones radicales

                 

 

Habilidades para desarrollar

 

Al final de esta sección, podrá:

 
         
  • Divide expresiones radicales
    •      
  • Racionalizar un denominador de un término
    •      
  • Racionalizar un denominador de dos términos
    •  
 
 

Antes de comenzar, realiza este cuestionario de preparación.

 
 
         
  1. Simplifique: ( frac {30} {48} ).
    Si se perdió este problema, revise el Ejemplo 1.24.
    2.      
  2. Simplifique: (x ^ {2} ⋅x ^ {4} ).
    Si se perdió este problema, revise el Ejemplo 5.12.
    3.      
  3. Multiplicar: ((7 + 3x) (7−3x) ).
    Si se perdió este problema, revise el Ejemplo 5.32.
    4.  
 
 
 

Dividir expresiones radicales

 

Hemos utilizado la Propiedad del cociente de las expresiones radicales para simplificar las raíces de las fracciones. Tendremos que usar esta propiedad “a la inversa” para simplificar una fracción con radicales. Le damos de nuevo la propiedad del cociente de las expresiones radicales para una fácil referencia. Recuerde, asumimos que todas las variables son mayores o iguales a cero, por lo que no se necesitan barras de valor absoluto.

 
 

Definición ( PageIndex {1} ): Propiedad del cociente de expresiones radicales

 

Si ( sqrt [n] {a} ) y ( sqrt [n] {b} ) son números reales, (b ≠ 0 ) y para cualquier número entero (n≥2 ) entonces,

 

( sqrt [n] { frac {a} {b}} = frac { sqrt [n] {a}} { sqrt [n] {b}} quad text {y} quad frac { sqrt [n] {a}} { sqrt [n] {b}} = sqrt [n] { frac {a} {b}} )

 
 
 

Usaremos la propiedad del cociente de las expresiones radicales cuando la fracción con la que comenzamos es el cociente de dos radicales, y ninguno de los dos radicandos es una potencia perfecta del índice. Cuando escribimos la fracción en un solo radical, podemos encontrar factores comunes en el numerador y el denominador.

 
 

Ejemplo ( PageIndex {1} )

 

Simplificar:

 
         
  1. ( frac { sqrt {72 x ^ {3}}} { sqrt {162 x}} )
    2.      
  2. ( frac { sqrt [3] {32 x ^ {2}}} { sqrt [3] {4 x ^ {5}}} )
    3.  
 

Solución :

 

a.

 

( frac { sqrt {72 x ^ {3}}} { sqrt {162 x}} )

 

Reescribe usando la propiedad del cociente,

 

( sqrt { frac {72 x ^ {3}} {162 x}} )

 

Eliminar los factores comunes.

 

( sqrt { frac { cancel {18} cdot 4 cdot x ^ {2} cdot cancel {x}} { cancel {18} cdot 9 cdot cancel {x} }} )

 

Simplificar.

 

( sqrt { frac {4 x ^ {2}} {9}} )

 

Simplifica el radical.

 

( frac {2 x} {3} )

 

b.

 

( frac { sqrt [3] {32 x ^ {2}}} { sqrt [3] {4 x ^ {5}}} )

 

Reescribe usando la propiedad del cociente, ( frac { sqrt [n] {a}} { sqrt [n] {b}} = sqrt [n] { frac {a} {b}} )

 

( sqrt [3] { frac {32 x ^ {2}} {4 x ^ {5}}} )

 

Simplifica la fracción bajo el radical.

 

( sqrt [3] { frac {8} {x ^ {3}}})

 

Simplifica el radical.

 

( frac {2} {x} )

 
 
 

Ejercicio ( PageIndex {1} )

 

Simplificar:

 
         
  1. ( frac { sqrt {50 s ^ {3}}} { sqrt {128 s}} )
    2.      
  2. ( frac { sqrt [3] {56 a}} { sqrt [3] {7 a ^ {4}}} )
    3.  
 
     
Respuesta
     
     
             
  1. ( frac {5s} {8} )
    2.          
  2. ( frac {2} {a} )
    3.      
     
 
 
 
 

Ejercicio ( PageIndex {2} )

 

Simplificar:

 
         
  1. ( frac { sqrt {75 q ^ {5}}} { sqrt {108 q}} )
    2.      
  2. ( frac { sqrt [3] {72 b ^ {2}}} { sqrt [3] {9 b ^ {5}}} )
    3.  
 
     
Respuesta
     
     
             
  1. ( frac {5 q ^ {2}} {6} )
    2.          
  2. ( frac {2} {b} )
    3.      
     
 
 
 
 

Ejemplo ( PageIndex {2} )

 

Simplificar:

 
         
  1. ( frac { sqrt {147 a b ^ {8}}} { sqrt {3 a ^ {3} b ^ {4}}} )
    2.      
  2. ( frac { sqrt [3] {- 250 m n ^ {- 2}}} { sqrt [3] {2 m ^ {- 2} n ^ {4}}} )
    3.  
 

Solución :

 

a.

 

( frac { sqrt {147 a b ^ {8}}} { sqrt {3 a ^ {3} b ^ {4}}} )

 

Reescribe usando la propiedad del cociente.

 

( sqrt { frac {147 a b ^ {8}} {3 a ^ {3} b ^ {4}}} )

 

Eliminar los factores comunes en la fracción.

 

( sqrt { frac {49 b ^ {4}} {a ^ {2}}} )

 

Simplifica el radical.

 

( frac {7 b ^ {2}} {a} )

 

b.

 

( frac { sqrt [3] {- 250 m n ^ {- 2}}} { sqrt [3] {2 m ^ {- 2} n ^ {4}}} )

 

Reescribe usando la propiedad del cociente.

 

( sqrt [3] { frac {-250 m n ^ {- 2}} {2 m ^ {- 2} n ^ {4}}} )

 

Simplifica la fracción bajo el radical.

 

( sqrt [3] { frac {-125 m ^ {3}} {n ^ {6}}} )

 

Simplifica el radical.

 

(- frac {5 m} {n ^ {2}} )

 
 
 

Ejercicio ( PageIndex {3} )

 

Simplificar:

 
         
  1. ( frac { sqrt {162 x ^ {10} y ^ {2}}} { sqrt {2 x ^ {6} y ^ {6}}} )
    2.      
  2. ( frac { sqrt [3] {- 128 x ^ {2} y ^ {- 1}}} { sqrt [3] {2 x ^ {- 1} y ^ {2}}} )
    3.  
 
     
Respuesta
     
     
             
  1. ( frac {9 x ^ {2}} {y ^ {2}} )
    2.          
  2. ( frac {-4 x} {y} )
    3.      
     
 
 
 
 

Ejercicio ( PageIndex {4} )

 

Simplificar:

 
         
  1. ( frac { sqrt {300 m ^ {3} n ^ {7}}} { sqrt {3 m ^ {5} n}} )
    2.      
  2. ( frac { sqrt [3] {- 81 p q ^ {- 1}}} { sqrt [3] {3 p ^ {- 2} q ^ {5}}} )
    3.  
 
     
Respuesta
     
     
             
  1. ( frac {10 n ^ {3}} {m} )
    2.          
  2. ( frac {-3 p} {q ^ {2}} )
    3.      
     
 
 
 
 

Ejemplo ( PageIndex {3} )

 

Simplifique: ( frac { sqrt {54 x ^ {5} y ^ {3}}} { sqrt {3 x ^ {2} y}} )

 

Solución :

 

( frac { sqrt {54 x ^ {5} y ^ {3}}} { sqrt {3 x ^ {2} y}} )

 

Reescribe usando la propiedad del cociente.

 

( sqrt { frac {54 x ^ {5} y ^ {3}} {3 x ^ {2} y}} )

 

Eliminar los factores comunes en la fracción.

 

( sqrt {18 x ^ {3} y ^ {2}} )

 

Reescribe el radicando como un producto usando el factor cuadrado perfecto más grande.

 

( sqrt {9 x ^ {2} y ^ {2} cdot 2 x} )

 

Reescribe el radical como el producto de dos radicales.

 

( sqrt {9 x ^ {2} y ^ {2}} cdot sqrt {2 x} )

 

Simplificar.

 

(3 x y sqrt {2 x} )

 
 
 

Ejercicio ( PageIndex {5} )

 

Simplifique: ( frac { sqrt {64 x ^ {4} y ^ {5}}} { sqrt {2 x y ^ {3}}} )

 
     
Respuesta
     
     

(4 x y sqrt {2 x} )

     
 
 
 
 

Ejercicio ( PageIndex {6} )

 

Simplifique: ( frac { sqrt {96 a ^ {5} b ^ {4}}} { sqrt {2 a ^ {3} b}} )

 
     
Respuesta
     
     

(4 a b sqrt {3 b} )

     
 
 
 

Racionalizar un denominador de un término

 

Antes de que la calculadora se convirtiera en una herramienta de la vida cotidiana, ¡aproximar el valor de una fracción con un radical en el denominador era un proceso muy engorroso!

 

Por esta razón, se desarrolló un proceso llamado racionalizando el denominador . Una fracción con un radical en el denominador se convierte en una fracción equivalente cuyo denominador es un entero. Las raíces cuadradas de los números que no son cuadrados perfectos son números irracionales. Cuando racionalizamos el denominador, escribimos una fracción equivalente con un número racional en el denominador. Este proceso todavía se usa hoy en día y también es útil en otras áreas de las matemáticas.

 
 

Definición ( PageIndex {2} ): Racionalizar el denominador

 

Racionalizar el denominador es el proceso de convertir una fracción con un radical en el denominador en una fracción equivalente cuyo denominador es un entero.

 
 

Aunque tenemos calculadoras disponibles en casi todas partes, una fracción con un radical en el denominador todavía debe racionalizarse. No se considera simplificado si el denominador contiene un radical.

 

Del mismo modo, una expresión radical no se considera simplificada si el radicando contiene una fracción.

 

Expresiones radicales simplificadas

 

Una expresión radical se considera simplificada si hay

 
         
  • no hay factores en el radio y tienen poderes perfectos del índice
    •      
  • sin fracciones en el radio y
    •      
  • sin radicales en el denominador de una fracción
    •  
 

Para racionalizar un denominador con una raíz cuadrada, utilizamos la propiedad que (( sqrt {a}) ^ {2} = a ). Si elevamos al cuadrado una raíz cuadrada irracional, obtenemos un número racional.

 

Usaremos esta propiedad para racionalizar el denominador en el siguiente ejemplo.

 
 

Ejemplo ( PageIndex {4} )

 

Simplificar:

 
         
  1. ( frac {4} { sqrt {3}} )
    2.      
  2. ( sqrt { frac {3} {20}} )
    3.      
  3. ( frac {3} { sqrt {6 x}} )
    4.  
 

Solución :

 

Para racionalizar un denominador con un término, podemos multiplicar una raíz cuadrada por sí mismo. Para mantener la fracción equivalente, multiplicamos tanto el numerador como el denominador por el mismo factor.

 

a.

                                                                                                                                                              
             

.

             
Multiplica el numerador y el denominador por ( sqrt {3} ).              

.

             
Simplifica.              

.

             
 

Tabla 8.5.1

 

b. Siempre simplificamos el radical en el denominador primero, antes de racionalizarlo. De esta manera, los números se mantienen más pequeños y más fáciles de trabajar.

                                                                                                                                                                                                                                                                                                              
             

.

             
La fracción no es un cuadrado perfecto, así que reescribe usando la Propiedad del cociente.              

.

             
Simplifica el denominador.              

.

             
Multiplica el numerador y el denominador por ( sqrt {5} ).              

.

             
Simplifica.              

.

             
Simplifica.              

.

             
 

Tabla 8.5.2

 

c.

                                                                                                                                                                                                              
             

.

             
Multiplica el numerador y el denominador por ( sqrt {6x} ).              

.

             
Simplifica.              

.

             
Simplifica.              

.

             
 

Tabla 8.5.3

 
 
 

Ejercicio ( PageIndex {7} )

 

Simplificar:

 
         
  1. ( frac {5} { sqrt {3}} )
    2.      
  2. ( sqrt { frac {3} {32}} )
    3.      
  3. ( frac {2} { sqrt {2 x}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac {5 sqrt {3}} {3} )
    2.          
  2. ( frac { sqrt {6}} {8} )
    3.          
  3. ( frac { sqrt {2 x}} {x} )
    4.      
     
 
 
 
 

Ejercicio ( PageIndex {8} )

 

Simplificar:

 
         
  1. ( frac {6} { sqrt {5}} )
    2.      
  2. ( sqrt { frac {7} {18}} )
    3.      
  3. ( frac {5} { sqrt {5 x}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac {6 sqrt {5}} {5} )
    2.          
  2. ( frac { sqrt {14}} {6} )
    3.          
  3. ( frac { sqrt {5 x}} {x} )
    4.      
     
 
 
 

Cuando racionalizamos una raíz cuadrada, multiplicamos el numerador y el denominador por una raíz cuadrada que nos daría un cuadrado perfecto debajo del radical en el denominador. Cuando sacamos la raíz cuadrada, el denominador ya no tenía un radical.

 

Seguiremos un proceso similar para racionalizar raíces superiores. Para racionalizar un denominador con un radical índice más alto, multiplicamos el numerador y el denominador por un radical que nos daría un radical y que es una potencia perfecta del índice. Cuando simplificamos el nuevo radical, el denominador ya no tendrá un radical.

 

Por ejemplo,

 
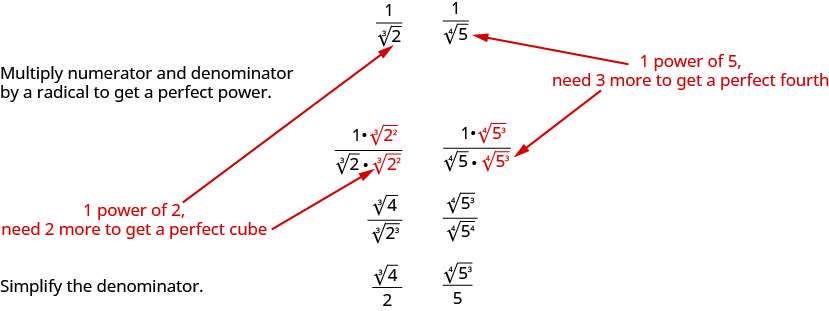
Two examples of rationalizing denominators are shown. The first example is 1 divided by cube root 2. A note is made that the radicand in the denominator is 1 power of 2 and that we need 2 more to get a perfect cube. We multiply numerator and denominator by the cube root of the quantity 2 squared. The result is cube root 4 divided by cube root of quantity 2 cubed. This simplifies to cube root 4 divided by 2. The second example is 1 divided by fourth root 5. A note is made that the radicand in the denominator is 1 power of 5 and that we need 3 more to get a perfect fourth. We multiply numerator and denominator by the fourth root of the quantity 5 cubed. The result is fourth root of 125 divided by fourth root of quantity 5 to the fourth. This simplifies to fourth root 125 divided by 5.  
Figura 8.5.14
 
 

Utilizaremos esta técnica en los siguientes ejemplos.

 
 

Ejemplo ( PageIndex {5} )

 

Simplificar:

 
         
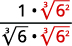
  1. ( frac {1} { sqrt [3] {6}} )
    2.      
  2. ( sqrt [3] { frac {7} {24}} )
    3.      
  3. ( frac {3} { sqrt [3] {4 x}} )
    4.  
 

Solución :

 

Para racionalizar un denominador con una raíz cúbica, podemos multiplicar por una raíz cúbica que nos dará un cubo perfecto en el radio y en el denominador. Para mantener la fracción equivalente, multiplicamos tanto el numerador como el denominador por el mismo factor.

 

a.

                                                                                                                                                                                                              
             

.

             
El radical en el denominador tiene un factor de (6 ). Multiplique tanto el numerador como el denominador por ( sqrt [3] {6 ^ {2}} ), lo que nos da (2 ) más factores de (6 ).              

.

             
Multiplica. Observe que el radicando en el denominador tiene (3 ) poderes de (6 ).              

.

             
Simplifica la raíz cúbica en el denominador.              

.

             
 

Tabla 8.5.4

 

b. Siempre simplificamos el radical en el denominador primero, antes de racionalizarlo. De esta manera, los números se mantienen más pequeños y más fáciles de trabajar.

                                                                                                                                                                                                                                                                                                                                                              
             

.

             
La fracción no es un cubo perfecto, así que reescribe usando la Propiedad del cociente.              

.

             
Simplifica el denominador.              

.

             
Multiplica el numerador y el denominador por ( sqrt [3] {3 ^ {2}} ). Esto nos dará (3 ) factores de (3 ).              

.

             
Simplifica.              

.

             
Recuerde, ( sqrt [3] {3 ^ {3}} = 3 ).              

.

             
Simplifica.              

.

             
 

Tabla 8.5.5

 

c.

                                                                                                                                                                                                                                                              
             

.

             
Reescribe el radicando para mostrar los factores.              

.

             
Multiplica el numerador y el denominador por ( sqrt [3] {2 cdot x ^ {2}} ). Esto nos dará (3 ) factores de (2 ) y (3 ) factores de (x ).              

.

             
Simplifica.              

.

             
Simplifica el radical en el denominador.              

.

             
 

Tabla 8.5.6

 
 
 

Ejercicio ( PageIndex {9} )

 

Simplificar:

 
         
  1. ( frac {1} { sqrt [3] {7}} )
    2.      
  2. ( sqrt [3] { frac {5} {12}} )
    3.      
  3. ( frac {5} { sqrt [3] {9 y}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac { sqrt [3] {49}} {7} )
    2.          
  2. ( frac { sqrt [3] {90}} {6} )
    3.          
  3. ( frac {5 sqrt [3] {3 y ^ {2}}} {3 y} )
    4.      
     
 
 
 
 

Ejercicio ( PageIndex {10} )

 

Simplificar:

 
         
  1. ( frac {1} { sqrt [3] {2}} )
    2.      
  2. ( sqrt [3] { frac {3} {20}} )
    3.      
  3. ( frac {2} { sqrt [3] {25 n}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac { sqrt [3] {4}} {2} )
    2.          
  2. ( frac { sqrt [3] {150}} {10} )
    3.          
  3. ( frac {2 sqrt [3] {5 n ^ {2}}} {5 n} )
    4.      
     
 
 
 
 

Ejemplo ( PageIndex {6} )

 

Simplificar:

 
         
  1. ( frac {1} { sqrt [4] {2}} )
    2.      
  2. ( sqrt [4] { frac {5} {64}} )
    3.      
  3. ( frac {2} { sqrt [4] {8 x}} )
    4.  
 

Solución :

 

Para racionalizar un denominador con una cuarta raíz, podemos multiplicar por una cuarta raíz que nos dará una cuarta potencia perfecta en el radicando en el denominador. Para mantener la fracción equivalente, multiplicamos tanto el numerador como el denominador por el mismo factor.

 

a.

                                                                                                                                                                                                              
             

.

             
El radical en el denominador tiene un factor de (2 ).
Multiplica tanto el numerador como el denominador por ( sqrt [4] {2 ^ {3}} ), lo que nos da (3 ) más factores de (2 ). 		             

.

             
Multiplica. Observe que el radicando en el denominador tiene (4 ) poderes de (2 ).              

.

             
Simplifica la cuarta raíz en el denominador.              

.

             
 

Tabla 8.5.7

 

b. Siempre simplificamos el radical en el denominador primero, antes de racionalizarlo. De esta manera, los números se mantienen más pequeños y más fáciles de trabajar.

                                                                                                                                                                                                                                                                                                                                                                                                              
             

.

             
La fracción no es una cuarta potencia perfecta, así que reescribe usando la Propiedad del cociente.              

.

             
Reescribe el radicando en el denominador para mostrar los factores.              

.

             
Simplifica el denominador.              

.

             
Multiplica el numerador y el denominador por ( sqrt [4] {2 ^ {2}} ). Esto nos dará (4 ) factores de (2 ).              

.

             
Simplifica.              

.

             
Recuerde, ( sqrt [4] {2 ^ {4}} = 2 ).              

.

             
Simplifica.              

.

             
 

Tabla 8.5.8

 

c.

                                                                                                                                                                                                                                                                                                              
             

.

             
Reescribe el radicando para mostrar los factores.              

.

             
Multiplica el numerador y el denominador por ( sqrt [4] {2 cdot x ^ {3}} ). Esto nos dará (4 ) factores de (2 ) y (4 ) factores de (x ).              

.

             
Simplifica.              

.

             
Simplifica el radical en el denominador.              

.

             
Simplifica la fracción.              

.

             
 

Tabla 8.5.9

 
 
 

Ejercicio ( PageIndex {11} )

 

Simplificar:

 
         
  1. ( frac {1} { sqrt [4] {3}} )
    2.      
  2. ( sqrt [4] { frac {3} {64}} )
    3.      
  3. ( frac {3} { sqrt [4] {125 x}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac { sqrt [4] {27}} {3} )
    2.          
  2. ( frac { sqrt [4] {12}} {4} )
    3.          
  3. ( frac {3 sqrt [4] {5 x ^ {3}}} {5 x} )
    4.      
     
 
 
 
 

Ejercicio ( PageIndex {12} )

 

Simplificar:

 
         
  1. ( frac {1} { sqrt [4] {5}} )
    2.      
  2. ( sqrt [4] { frac {7} {128}} )
    3.      
  3. ( frac {4} { sqrt [4] {4 x}} )
    4.  
 
     
Respuesta
     
     
             
  1. ( frac { sqrt [4] {125}} {5} )
    2.          
  2. ( frac { sqrt [4] {224}} {8} )
    3.          
  3. ( frac { sqrt [4] {64 x ^ {3}}} {x} )
    4.      
     
 
 
 

Racionalizar un denominador de dos términos

 

Cuando el denominador de una fracción es una suma o diferencia con raíces cuadradas, utilizamos el Producto del patrón de conjugados para racionalizar el denominador .

 

( begin {array} {cc} {(ab) (a + b)} & {(2- sqrt {5}) (2+ sqrt {5})} \ {a ^ { 2} -b ^ {2}} y {2 ^ {2} – ( sqrt {5}) ^ {2}} \ {} y {4-5} \ {} y {- 1} end {array} )

 

Cuando multiplicamos un binomio que incluye una raíz cuadrada por su conjugado, el producto no tiene raíces cuadradas.

 
 

Ejemplo ( PageIndex {7} )

 

Simplifique: ( frac {5} {2- sqrt {3}} )

 

Solución :

 

Tabla 8.5.10

 
 
 

Ejercicio ( PageIndex {13} )

 

Simplifique: ( frac {3} {1- sqrt {5}} ).

 
     
Respuesta
     
     

(- frac {3 (1+ sqrt {5})} {4} )

     
 
 
 
 

Ejercicio ( PageIndex {14} )

 

Simplifique: ( frac {2} {4- sqrt {6}} ).

 
     
Respuesta
     
     

( frac {4+ sqrt {6}} {5} )

     
 
 
 

Observe que no distribuimos (5 ) en la respuesta del último ejemplo. Al dejar el resultado factorizado, podemos ver si hay algún factor que pueda ser común tanto para el numerador como para el denominador.

 
 

Ejemplo ( PageIndex {8} )

 

Simplifique: ( frac { sqrt {3}} { sqrt {u} – sqrt {6}} ).

 

Solución :

                                                                                                                                                                                                              
.
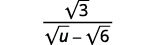Multiplica el numerador y el denominador por el conjugado del denominador. .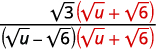
Multiplica los conjugados en el denominador. .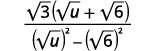
Simplifica el denominador. .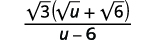
 

Tabla 8.5.11

 
 
 

Ejercicio ( PageIndex {15} )

 

Simplifique: ( frac { sqrt {5}} { sqrt {x} + sqrt {2}} ).

 
     
Respuesta
     
     

( frac { sqrt {5} ( sqrt {x} – sqrt {2})} {x-2} )

     
 
 
 
 

Ejercicio ( PageIndex {16} )

 

Simplifique: ( frac { sqrt {10}} { sqrt {y} – sqrt {3}} )

 
     
Respuesta
     
     

( frac { sqrt {10} ( sqrt {y} + sqrt {3})} {y-3} )

     
 
 
 

Tenga cuidado con los signos al multiplicar. El numerador y el denominador se ven muy similares cuando multiplicas por el conjugado.

 
 

Ejemplo ( PageIndex {9} )

 

Simplifique: ( frac { sqrt {x} + sqrt {7}} { sqrt {x} – sqrt {7}} ).

 

Solución :

                                                                                                                                                                                                              
.
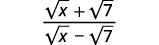Multiplica el numerador y el denominador por el conjugado del denominador. .
Multiplica los conjugados en el denominador. .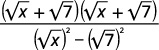
Simplifica el denominador. .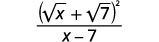
 

Tabla 8.5.12

 

No cuadramos el numerador. Dejándolo en forma factorizada, podemos ver que no hay factores comunes para eliminar del numerador y el denominador.

 
 
 

Ejercicio ( PageIndex {17} )

 

Simplifique: ( frac { sqrt {p} + sqrt {2}} { sqrt {p} – sqrt {2}} ).

 
     
Respuesta
     
     

( frac {( sqrt {p} + sqrt {2}) ^ {2}} {p-2} )

     
 
 
 
 

Ejercicio ( PageIndex {18} )

 

Simplifique: ( frac { sqrt {q} – sqrt {10}} { sqrt {q} + sqrt {10}} )

 
     
Respuesta
     
     

( frac {( sqrt {q} – sqrt {10}) ^ {2}} {q-10} )

     
 
 
 

Acceda a estos recursos en línea para obtener instrucción adicional y practicar dividiendo expresiones radicales.

 

Conceptos clave

 
         
  • Propiedad del cociente de expresiones radicales      
               
    • Si ( sqrt [n] {a} ) y ( sqrt [n] {b} ) son números reales, (b ≠ 0 ), y para cualquier número entero (n≥2 ) entonces, ( sqrt [n] { frac {a} {b}} = frac { sqrt [n] {a}} { sqrt [n] {b}} ) y ( frac { sqrt [n] {a}} { sqrt [n] {b}} = sqrt [n] { frac {a} {b}} )
      •      
         
    •      
  • Expresiones radicales simplificadas      
               
    • Una expresión radical se considera simplificada si hay:          
                     
      • no hay factores en el radio y que tienen poderes perfectos del índice
        •              
      • sin fracciones en el radio y
        •              
      • sin radicales en el denominador de una fracción
        •          
               
      •      
         
    •  
 

 

Glosario

 
     
racionalizando el denominador
     
Racionalizar el denominador es el proceso de convertir una fracción con un radical en el denominador en una fracción equivalente cuyo denominador es un entero.
 
 
                                  
]]>

Post Views: 39